题目内容
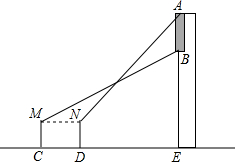 如图,小明在广场上的C处用测角仪正面测量一座楼房墙上的广告屏幕AB的长度,测得屏幕下端B处的仰角为30°,然后他正对大楼方向前进10米到达D处,又测得该屏幕上端A处的仰角为45°,已知该楼高18.7米,测角仪MC、ND的高度为1.7米,求广告屏幕AB的长.
如图,小明在广场上的C处用测角仪正面测量一座楼房墙上的广告屏幕AB的长度,测得屏幕下端B处的仰角为30°,然后他正对大楼方向前进10米到达D处,又测得该屏幕上端A处的仰角为45°,已知该楼高18.7米,测角仪MC、ND的高度为1.7米,求广告屏幕AB的长.考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点N作NF⊥AE于点F,设BF=x,根据题意可知∠BMF=30°,∠ANF=45°,分别在Rt△BMF和Rt△ANF中求出MF、AF的长度,根据楼高为18.7米可得AF+EF=18.7米,代入求出x的值,继而可求得AB的长度.
解答: 解:过点N作NF⊥AE于点F,
解:过点N作NF⊥AE于点F,
则四边形NDEF为矩形,ND=EF,
设BF=x米,
在Rt△BMF中,
∵∠BMF=30°,
∴MF=
BF=
x,
∵MN=10米,
∴NF=
x-10,
∵∠ANF=45°,
∴AF=NF=
x-10,
∴
x-10+1.7=18.7,
解得:x=9
,
则AB=AF-BF=27-9
.
即广告屏幕AB的长度为(27-9
)米.
 解:过点N作NF⊥AE于点F,
解:过点N作NF⊥AE于点F,则四边形NDEF为矩形,ND=EF,
设BF=x米,
在Rt△BMF中,
∵∠BMF=30°,
∴MF=
| 3 |
| 3 |
∵MN=10米,
∴NF=
| 3 |
∵∠ANF=45°,
∴AF=NF=
| 3 |
∴
| 3 |
解得:x=9
| 3 |
则AB=AF-BF=27-9
| 3 |
即广告屏幕AB的长度为(27-9
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡度和仰角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
在同一平面直角坐标系中,将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位后再沿y轴向下平移1个单位,得到图象的顶点坐标是( )
| A、(-1,1) |
| B、(1,-2) |
| C、(2,-2) |
| D、(1,-2) |

 已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数y=
已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数y=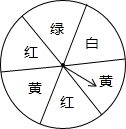 如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题:
如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题: