题目内容
设棱锥的顶点数为V,面数为F,棱数为E.
(1)观察与发现:三棱锥中,V3= ,F3= ,E3= ;
五棱锥中,V5= ,F5= ,E5= ;
(2)猜想:①十棱锥中,V10= ,F10= ,E10= ;
②n棱锥中,Vn= ,Fn= ,En= ;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系: ;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E= ;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.

(1)观察与发现:三棱锥中,V3=
五棱锥中,V5=
(2)猜想:①十棱锥中,V10=
②n棱锥中,Vn=
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系:
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E=
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.

考点:欧拉公式
专题:
分析:(1)观察与发现:根据三棱锥、五棱锥的特征填写即可;
(2)猜想:①根据十棱锥的特征填写即可;
②根据n棱锥的特征的特征填写即可;
(3)探究:①通过列举得到棱锥的顶点数(V)与面数(F)之间的等量关系;
②通过列举得到棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系;
(4)拓展:根据棱柱的特征得到棱柱的顶点数(V)、面数(F)、棱数(E)之间的等量关系.
(2)猜想:①根据十棱锥的特征填写即可;
②根据n棱锥的特征的特征填写即可;
(3)探究:①通过列举得到棱锥的顶点数(V)与面数(F)之间的等量关系;
②通过列举得到棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系;
(4)拓展:根据棱柱的特征得到棱柱的顶点数(V)、面数(F)、棱数(E)之间的等量关系.
解答:解:(1)观察与发现:三棱锥中,V3=4,F3=4,E3=6;
五棱锥中,V5=5,F5=5,E5=8;
(2)猜想:①十棱锥中,V10=11,F10=11,E10=20;
②n棱锥中,Vn=n+1,Fn=n+1,En=2n;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系:V=F;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E=V+F-E=2;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间也存在某种等量关系,相应的等式是:V+F-E=2.
故答案为:4,4,6;5,5,8;11,11,20;n+1,n+1,2n;V=F,V+F-E=2.
五棱锥中,V5=5,F5=5,E5=8;
(2)猜想:①十棱锥中,V10=11,F10=11,E10=20;
②n棱锥中,Vn=n+1,Fn=n+1,En=2n;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系:V=F;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E=V+F-E=2;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间也存在某种等量关系,相应的等式是:V+F-E=2.
故答案为:4,4,6;5,5,8;11,11,20;n+1,n+1,2n;V=F,V+F-E=2.
点评:考查了欧拉公式,本题由几个特殊多面体,观察它们的顶点数、面数和棱数,归纳出一般结论,得到欧拉公式,着重考查了归纳推理和多面体的性质等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法正确的是( )
| A、一个角的补角一定大于这个角 |
| B、锐角和钝角互补 |
| C、直线AB与直线BA是同一直线 |
| D、射线AB与射线BA是同一射线 |
已知x2-kxy+64y2是一个完全平方式,则k的值是( )
| A、8 | B、±8 | C、±16 | D、16 |
 如果有理数x、y在数轴上的位置如图,那么下列关系式
如果有理数x、y在数轴上的位置如图,那么下列关系式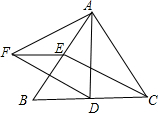 如图,△ABC为等边三角形,D、E分别是BC、AB上的点,且CD=BE,以AD为边作等边△AFD
如图,△ABC为等边三角形,D、E分别是BC、AB上的点,且CD=BE,以AD为边作等边△AFD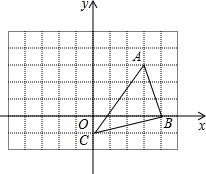 如图,点A的坐标为(3,3),点B的坐标为(4,0).点C的坐标为(0,-1).
如图,点A的坐标为(3,3),点B的坐标为(4,0).点C的坐标为(0,-1). 如图,已知AC∥BD,∠2=∠3.求证:AB∥CD.
如图,已知AC∥BD,∠2=∠3.求证:AB∥CD.