题目内容
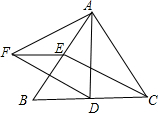 如图,△ABC为等边三角形,D、E分别是BC、AB上的点,且CD=BE,以AD为边作等边△AFD
如图,△ABC为等边三角形,D、E分别是BC、AB上的点,且CD=BE,以AD为边作等边△AFD(1)判断△ACD与△CBE的关系并证明;
(2)判断EF与DC的关系,并证明你的结论.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)等边三角形的性质就可以得出△ACD≌△CBE而得出结论.
(2)连接BF,由等式的性质就可以求出∠BAF=∠CAD,进而证明△BAF≌△CAD就可以得出BF=CD,∠ABF=∠ACD=60°就可以得出结论.
(2)连接BF,由等式的性质就可以求出∠BAF=∠CAD,进而证明△BAF≌△CAD就可以得出BF=CD,∠ABF=∠ACD=60°就可以得出结论.
解答:解:(1)△ACD≌△CBE.
∵△ABC为等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠ACB=60°.
在△ACD和△CBE中
,
∴△ACD≌△CBE(SAS).
(2)EF=DC,EF∥DC.
连接BF,
∵△AFD是等边三角形,
∴AF=AD,∠DAF=60°.
∴∠DAF=∠CAB,
∴∠DAF-∠BAD=∠CAB-∠BAD,
∴∠BAF=∠CAD.
在△BAF和△CAD中
,
∴△BAF≌△CAD(SAS),
∴BF=CD,∠ABF=∠ACD=60°.
∵BE=CD,
∴BF=BE.
∴△BFE是等边三角形,
∴EF=BE,∠BEF=60°,
∴EF=DC,∠BEF=∠ABC,
∴EF∥BC,即EF∥CD.
∵△ABC为等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠ACB=60°.
在△ACD和△CBE中
|
∴△ACD≌△CBE(SAS).
(2)EF=DC,EF∥DC.
连接BF,
∵△AFD是等边三角形,
∴AF=AD,∠DAF=60°.
∴∠DAF=∠CAB,
∴∠DAF-∠BAD=∠CAB-∠BAD,

∴∠BAF=∠CAD.
在△BAF和△CAD中
|
∴△BAF≌△CAD(SAS),
∴BF=CD,∠ABF=∠ACD=60°.
∵BE=CD,
∴BF=BE.
∴△BFE是等边三角形,
∴EF=BE,∠BEF=60°,
∴EF=DC,∠BEF=∠ABC,
∴EF∥BC,即EF∥CD.
点评:本题考查了等边三角形的判定及性质的运用,全等三角形的判定及性质的运用,平行线的判定的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
当x=-1时,代数式2x2+5的值为( )
| A、7 | B、-7 | C、3 | D、-3 |
下列说法中正确的是( )
| A、36的平方根是6 |
| B、4的平方根是±2 |
| C、8的立方根是-2 |
| D、4的算术平方根是-2 |
泉州市地处福建省东南部,是福建省三大中心城市之一.少数民族有48个,以回族、畲族、苗族和蒙古族居多,2012年末常住人口8290000万人,将数8290000用科学记数法表示为( )
| A、829×104 |
| B、82.9×105 |
| C、8.29×106 |
| D、0.829×107 |
 如图,已知在△ABC中,AB=AC,∠A=20°,D,E分别为AC,AB上的点,∠DBC=60°,∠ECB=50°,则∠BDE=
如图,已知在△ABC中,AB=AC,∠A=20°,D,E分别为AC,AB上的点,∠DBC=60°,∠ECB=50°,则∠BDE=
 已知:如图,△ABC,请你用尺规作图法作出AB边上的高线.(要求保留作图痕迹)
已知:如图,△ABC,请你用尺规作图法作出AB边上的高线.(要求保留作图痕迹)