题目内容
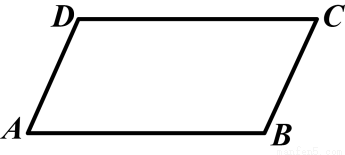
如图所示,在四边形ABCD中,AD∥BC,E是AD上一点,且AE=3,ED=2,BC=15,AB=8,DC=6,则AB与CD互相垂直吗?请说明理由.

【解析】
AB与CD互相垂直.理由是:
过点E分别作EF∥AB,EG∥DC,交BC于点F、G.
因为AD∥BC,所以AE∥BF,ED∥GC,
∴四边形ABFE,四边形EGCD都是平行四边形.
∴AB=EF=8,BF=AE=3,EG=DC=6,GC=ED=2,
∴FG=BC-BF-GC=15-3-2=10.
在△EFG中,EF2+EG2=82+62=100,FG2=102=100,
∴EF2+EG2=FG2.
∴△EFG为直角三角形.
∴EF⊥EG.∵EF∥AB,EG∥DC,所以AB⊥DC.

【解析】本题的关键点在于构造平行四边形,进而将AB线段平移,利用了平行四边形对边平行的性质。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

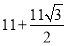
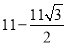
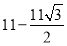
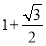


 ,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )