题目内容
解方程:
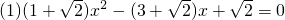
(2)20x2+253x+800=0;
(3)x2+|2x-1|-4=0.
解:(1)(1+ )x2-(3+
)x2-(3+ )x+
)x+ =0
=0
a=1+ ,b=-(3+
,b=-(3+ ),c=
),c=
△=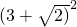 -4(1+
-4(1+ )×
)×
=3+2 =
=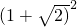 ,
,
x=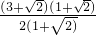 ,
,
x1= ,x2=
,x2= -1.
-1.
(2)20x2+253x+800=0,
a=20,b=253,c=800,
△=b2-4ac=2532-4×20×800=9,
x=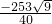 ,
,
x1=- ,x2=-
,x2=- .
.
(3)x2+|2x-1|-4=0,
当2x-1≥0,即x≥ 时,原方程为:x2+2x-5=0,
时,原方程为:x2+2x-5=0,
解方程得:x=-1± ,
,
∵-1- <
< ∴x=-1+
∴x=-1+ .
.
当2x-1<0,即x< 时,原方程为:x2-2x-3=0,
时,原方程为:x2-2x-3=0,
解方程得:x1=3,x2=-1,
∵3> ,∴x=-1.
,∴x=-1.
故原方程的根为:x1=-1+ ,x2=-1.
,x2=-1.
分析:(1)确定a,b,c的值,准确运用求根公式解方程;
(2)a,b,c的值较大,先求判别式△的值,再用公式求根;
(3)由于带有绝对值的符号,先讨论x的范围再求根.
点评:(1)(2)两题准确运用一元二次方程的求根公式求出方程的根,(3)题由于带有绝对值符号,分两个范围求出方程的根,对不合题意的根要舍去.
 )x2-(3+
)x2-(3+ )x+
)x+ =0
=0a=1+
 ,b=-(3+
,b=-(3+ ),c=
),c=
△=
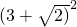 -4(1+
-4(1+ )×
)×
=3+2
 =
=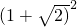 ,
,x=
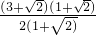 ,
,x1=
 ,x2=
,x2= -1.
-1.(2)20x2+253x+800=0,
a=20,b=253,c=800,
△=b2-4ac=2532-4×20×800=9,
x=
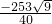 ,
,x1=-
 ,x2=-
,x2=- .
.(3)x2+|2x-1|-4=0,
当2x-1≥0,即x≥
 时,原方程为:x2+2x-5=0,
时,原方程为:x2+2x-5=0,解方程得:x=-1±
 ,
,∵-1-
 <
< ∴x=-1+
∴x=-1+ .
.当2x-1<0,即x<
 时,原方程为:x2-2x-3=0,
时,原方程为:x2-2x-3=0,解方程得:x1=3,x2=-1,
∵3>
 ,∴x=-1.
,∴x=-1.故原方程的根为:x1=-1+
 ,x2=-1.
,x2=-1.分析:(1)确定a,b,c的值,准确运用求根公式解方程;
(2)a,b,c的值较大,先求判别式△的值,再用公式求根;
(3)由于带有绝对值的符号,先讨论x的范围再求根.
点评:(1)(2)两题准确运用一元二次方程的求根公式求出方程的根,(3)题由于带有绝对值符号,分两个范围求出方程的根,对不合题意的根要舍去.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目