题目内容
3.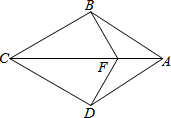 如图,在四边形ABCD中,AB=AD,CB=CD,点F是AC上一点,连结BF,DF.
如图,在四边形ABCD中,AB=AD,CB=CD,点F是AC上一点,连结BF,DF.(1)证明:△ABF≌△ADF;
(2)若AB∥CD,试证明四边形ABCD是菱形.
分析 (1)首先得出△ABC≌△ADC(SSS),进而利用全等三角形的性质得出∠BAC=∠DAC,再证明△ABF≌△ADF(SAS);
(2)利用平行线的性质得出∠BAC=∠DCA,进而得出AB=DC,再利用平行的判定方法得出答案.
解答 (1)证明:在△ABC和△ADC中
∵$\left\{\begin{array}{l}{AB=AD}\\{AC=AC}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中
∵$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠DAF}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ADF(SAS);
(2)解:∵AB∥CD,
∴∠BAC=∠DCA,
∵∠BAF=∠ADC,
∴∠DAC=∠DCA,
∴AD=DC,
由(1)得:AB=DC,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴平行四边形ABCD是菱形.
点评 此题主要考查了菱形的判定以及全等三角形的判定与性质,得出△ABC≌△ADC(SSS)是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.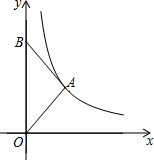 如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )
如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )
 如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )
如图,在平面直角坐标系中,点B在y轴上,第一象限内点A满足AB=AO,反比例函数y=$\frac{k}{x}$的图象经过点A,若△ABO的面积为2,则k的值为( )| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
15.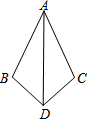 如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )
 如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )| A. | BD=DC | B. | AB=AC | C. | ∠B=∠C | D. | ∠BAD=∠CAD |
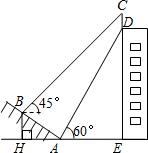 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡