题目内容
2.已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,依此类推,第2007个三角形的周长为$\frac{1}{{2}^{2006}}$.分析 易得第2个三角形的周长为$\frac{1}{2}$,那么第三个三角形的周长为($\frac{1}{2}$)2…第2007个三角形的周长为($\frac{1}{2}$)2007-1.
解答 解:根据三角形的中位线定理知:它的三条中位线组成的第二个三角形的周长是第一个三角形周长的一半,即$\frac{1}{2}$,
依此类推,则第2007个三角形的周长是($\frac{1}{2}$)2006=$\frac{1}{{2}^{2006}}$.
故答案是:$\frac{1}{{2}^{2006}}$.
点评 此题主要考查了三角形中位线的性质,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
 将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠AEG=70°,则∠BGE的度数为110°.
将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠AEG=70°,则∠BGE的度数为110°.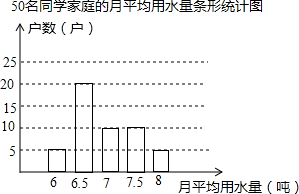 为了倡导“节约用水从我做起”,王伟同学在本校八年级的450名同学中,随机调查了50名同学家庭2012年1月至2012年10月的月平均用水量(单位:吨),并将调查结果绘成了下图所示的条形统计图.
为了倡导“节约用水从我做起”,王伟同学在本校八年级的450名同学中,随机调查了50名同学家庭2012年1月至2012年10月的月平均用水量(单位:吨),并将调查结果绘成了下图所示的条形统计图. 如图,直角梯形ABCD中,∠A=90°,∠B=120°,AD=$\sqrt{3}$,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长是2或5.
如图,直角梯形ABCD中,∠A=90°,∠B=120°,AD=$\sqrt{3}$,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长是2或5.