题目内容
12. 如图,直角梯形ABCD中,∠A=90°,∠B=120°,AD=$\sqrt{3}$,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长是2或5.
如图,直角梯形ABCD中,∠A=90°,∠B=120°,AD=$\sqrt{3}$,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长是2或5.
分析 过点B作BH⊥DC,延长AB至点M,过点C作CM⊥AB于F,则BH=AD=$\sqrt{3}$,再由锐角三角函数的定义求出CH及BC的长,设AE=x,则BE=6-x,利用勾股定理用x表示出DE及EF的长,再判断出△EDF∽△BCE,由相似三角形的对应边成比例即可得出关于x的方程,求出x的值即可.
解答 解:过点B作BH⊥DC,延长AB至点M,过点C作CM⊥AB于M,则BH=AD=MF=$\sqrt{3}$,
∵∠ABC=120°,AB∥CD,
∴∠BCH=60°,
∴CH=BM=$\frac{BH}{tan60°}$=1,
设AE=x,则BE=6-x,
在Rt△EFM中,EF=$\sqrt{(EB+BM)^{2}+M{F}^{2}}$=$\sqrt{(7-x)^{2}+3}$,
∵AB∥CD,
∴∠EFD=∠BEC,
∵∠DEF=∠B=120°,
∴△EDF∽△BCE,即△EDF∽△BFE,
∴$\frac{DF}{EF}=\frac{EF}{BE}$,
∴EF2=DF•BE,即(7-x)2+3=7(6-x),
解得x=2或5.
故答案为:2或5.
点评 本题考查了解直角梯形及相似三角形的判定与性质,勾股定理,特殊角的三角函数值等,解题的关键是根据题意画出图形,利用数形结合求解.

练习册系列答案
相关题目
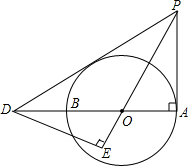 如图,AB是⊙O的直径,PA与⊙O相切于点A,PD交AB的延长线于点D,DE⊥PO交PO的延长线于点E,∠EPD=∠EDO
如图,AB是⊙O的直径,PA与⊙O相切于点A,PD交AB的延长线于点D,DE⊥PO交PO的延长线于点E,∠EPD=∠EDO 如图,在△ABC中,DE∥CB,若AD:DC=3:1,EB=2,则AE=6.
如图,在△ABC中,DE∥CB,若AD:DC=3:1,EB=2,则AE=6.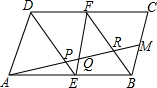 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、EF.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、EF.