题目内容
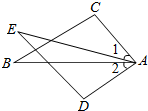 如图,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
如图,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定
专题:
分析:先由1=∠2得到∠CAB=∠DAE,然后分别利用“SAS”、“ASA”和“AAS”对各添加的条件进行判断.
解答:解:∵1=∠2,
∴∠CAB=∠DAE,
∵AC=AD,
∴当AB=AE时,可根据“SAS”判断△ABC≌△AED;
当BC=ED时,不能判断△ABC≌△AED;
当∠C=∠D时,可根据“ASA”判断△ABC≌△AED;
当∠B=∠E时,可根据“AAS”判断△ABC≌△AED.
故选C.
∴∠CAB=∠DAE,
∵AC=AD,
∴当AB=AE时,可根据“SAS”判断△ABC≌△AED;
当BC=ED时,不能判断△ABC≌△AED;
当∠C=∠D时,可根据“ASA”判断△ABC≌△AED;
当∠B=∠E时,可根据“AAS”判断△ABC≌△AED.
故选C.
点评:本题考查了全等三角形的判定:三条边分别对应相等的两个三角形全等;两边及其夹角分别对应相等的两个三角形全等;两角及其夹边分别对应相等的两个三角形全等;两角及其中一个角的对边对应相等的两个三角形全等.

练习册系列答案
相关题目
在平面直角坐标系中,将抛物线y=x2+1向右平移2个单位,再向下平移4个单位,得到的抛物线的解析式是( )
| A、y=(x+2)2-3 |
| B、y=(x-2)2-3 |
| C、y=(x-2)2+5 |
| D、y=(x+2)2+5 |
 如图,当一个点从O出发,沿15°线移动1个单位长度(即OP长为1个单位长度),这个点在竖直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,sin15°约等于( )
如图,当一个点从O出发,沿15°线移动1个单位长度(即OP长为1个单位长度),这个点在竖直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,sin15°约等于( )| A、3.73 | B、0.97 |
| C、0.50 | D、0.26 |
当地面高于海平面1米时,记作“+1米”,那么地面低于海平面10米时,记作( )
| A、-1米 | B、+1米 |
| C、-10米 | D、+10米 |
已知数a,b在数轴上表示的点的位置如图所示,则下列结论正确的是( )

①a<b<0;②|a|<|b|;③
<0;④b-a>a+b.

①a<b<0;②|a|<|b|;③
| a |
| b |
| A、①② | B、①④ | C、②③ | D、③④ |
 有理数a、b在数轴上对应的位置如图所示,则( )
有理数a、b在数轴上对应的位置如图所示,则( )| A、a+b>0 |
| B、a+b<0 |
| C、a+b=0 |
| D、a-b>0 |
 如图,O为直线AB上的一点,OE,OF分别平分∠AOC,∠COB,请问OE⊥OF吗?为什么?
如图,O为直线AB上的一点,OE,OF分别平分∠AOC,∠COB,请问OE⊥OF吗?为什么? 如图,点A、E、F、C线上,AD∥BC,AD=CB,AE=CE,求证:∠B=∠D.
如图,点A、E、F、C线上,AD∥BC,AD=CB,AE=CE,求证:∠B=∠D. 如图,已知AB∥CD,PA、PC分别平分∠BAC和∠ACD,试判断△APC的形状,并说明理由.
如图,已知AB∥CD,PA、PC分别平分∠BAC和∠ACD,试判断△APC的形状,并说明理由.