题目内容
3.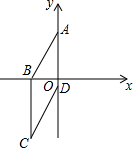 四边形ABCD为菱形,已知A(0,4),B(-3,0),求直线OC的解析式.
四边形ABCD为菱形,已知A(0,4),B(-3,0),求直线OC的解析式.
分析 先利用勾股定理计算出AB=5,再根据菱形的性质得到BC=5,从而确定C点坐标,然后利用待定系数法确定直线解析式即可.
解答 解:∵A(0,4),B(-3,0),
∴OA=4,OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∵四边形ABCD为菱形,
∴CB⊥BD,BC=BA=5,
∴C点坐标为(-3,-5),
设经过C点的直线例函数解式为y=kx(k为常数,k≠0),
把C(-3,-5)代入得k=$\frac{5}{3}$,
∴直线OC的解析式为y=$\frac{5}{3}$x.
点评 本题考查了菱形的性质、勾股定理的运用以及利用待定系数法求正比例函数的解析式,解题的关键是正确求出点C的坐标.

练习册系列答案
相关题目
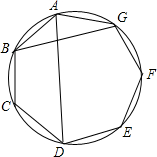 已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a-b)=ab2.
已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a-b)=ab2. 正方形ABCD边长为4,P(不与D重合)为DC边上一动点,设DP=x,求△APD的面积y关于x的函数,并写出x的取值范围.
正方形ABCD边长为4,P(不与D重合)为DC边上一动点,设DP=x,求△APD的面积y关于x的函数,并写出x的取值范围.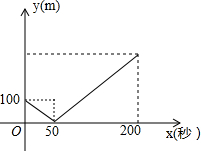 甲乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙千米,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点400米,其中正确的说法有( )
甲乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙千米,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点400米,其中正确的说法有( )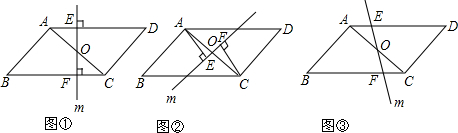
 画出几何体的主视图、左视图和俯视图.
画出几何体的主视图、左视图和俯视图.