题目内容
如图，在△ABC中，点D在边AC上，DB=BC，E是CD的中点，F是AB的中点，求证：EF=| 1 |
| 2 |
考点：直角三角形斜边上的中线,等腰三角形的性质
专题：证明题
分析：连接BE，根据等腰三角形三线合一的性质可得BE⊥AC，再根据直角三角形斜边上的中线等于斜边的一半证明．
解答：
证明：如图，连接BE，
∵在△BCD中，DB=BC，E是CD的中点，
∴BE⊥CD，
∵F是AB的中点，
∴在Rt△ABE中，EF是斜边AB上的中线，
∴EF=
AB．
证明：如图，连接BE，∵在△BCD中，DB=BC，E是CD的中点，
∴BE⊥CD，
∵F是AB的中点，
∴在Rt△ABE中，EF是斜边AB上的中线，
∴EF=
| 1 |
| 2 |
点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，熟记性质并作辅助线构造出直角三角形是解题的关键．
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
如图，点BD和CE分别在∠A的两边上，BE⊥AC于E点，CD⊥AB于D点，BE和CD相交于点F，图中有几对相似三角形，并任你选两对说明理由．下列函数的图象中，开口最小的是（ ）
| A、y=-4x2 | ||
| B、y=-2x2 | ||
C、y=
| ||
D、y=
|
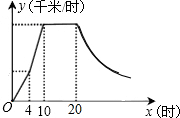某气象研究中心观测到一场沙尘暴从发生到减弱的过程，开始一段时间风速平均每小时增加2千米，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米，然后风速不变，当沙尘暴遇到绿色植被区时，风速y（小时/千米），时间x（小时）成反比例关系地慢慢减弱，结合风速与时间的图象，回答下列问题：