题目内容
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
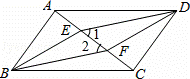
解:方法一:
补充条件①BE∥DF.
证明:如图,∵BE∥DF,
∴∠BEC=∠DFA,
∴∠BEA=∠DFC,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE与△CDF中,
 ,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴四边形BFDE是平行四边形,
∴ED∥BF,
∴∠1=∠2;
方法二:
补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF与△CDE中,

∴△ABF≌△CDE(SAS),
∴∠1=∠2.


练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
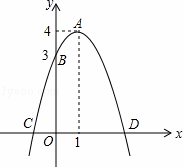
 =0,那么菱形的面积等于 .
=0,那么菱形的面积等于 . 其对角线,过点D作AC的平行线与BC的延长线交于E.
其对角线,过点D作AC的平行线与BC的延长线交于E.
 =
= (B)
(B) (C)
(C) (D)
(D)

 积为50m2的矩形场地,
积为50m2的矩形场地, 求矩形的长和宽各是多少.
求矩形的长和宽各是多少.
