题目内容
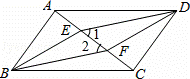
如图:在▱ABCD中,AC为 其对角线,过点D作AC的平行线与BC的延长线交于E.
其对角线,过点D作AC的平行线与BC的延长线交于E.
(1)求证:△ABC≌△DCE;
(2)若AC=BC,求证:四边形ACED为菱形.

证明:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠1,
又∵DE∥AC
∴∠2=∠E,
在△ABC与△DCE中,
 ,
,
∴△ABC≌△DCE;
(2)∵平行四边形ABCD中,
∴AD∥BC,
即AD∥CE,
由DE∥AC,
∴ACED为平行四边形,
∵AC=BC,
∴∠B=∠CAB,
由AB∥CD,
∴∠CAB=∠ACD,
又∵∠B=∠ADC,
∴∠ADC=∠ACD,
∴AC=AD,
∴四边形ACED为菱形.


练习册系列答案
相关题目

 cm B.2
cm B.2 cm C.2
cm C.2 cm D. 3cm
cm D. 3cm =55%,所以合并后的男生占总人数的55%.」如果是你,你会怎么列式求出合并后男生在总人数中占的百分比?你认为小清的答案在任何情况都对吗?请指出你认为小清的答案会对的情况.请依据你的列式检验你指出的情况下小清的答案会对的理由.
=55%,所以合并后的男生占总人数的55%.」如果是你,你会怎么列式求出合并后男生在总人数中占的百分比?你认为小清的答案在任何情况都对吗?请指出你认为小清的答案会对的情况.请依据你的列式检验你指出的情况下小清的答案会对的理由.
 为⊙
为⊙ 的内接三角形,
的内接三角形,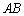 为⊙
为⊙
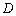 在⊙
在⊙ =55°,则
=55°,则 的大小等于
的大小等于
 (
( )的图象如图所示,
)的图象如图所示, ,有下列结论:①
,有下列结论:① <0;
<0;
 <0;③
<0;③ <
< .
. 圆柱 B.
圆柱 B.  正方体 C.
正方体 C.  圆锥 D.
圆锥 D.  球
球 =1.73);
=1.73);