题目内容
11. 某种商品的商标图案是如图所示的阴影部分,已知菱形ABCD的边长为8cm,∠A=60°.$\widehat{BD}$是以A为圆心.AB为半径的弧.$\widehat{CD}$是以B为圆心.BC为半径的弧,求该商标图案的面积.
某种商品的商标图案是如图所示的阴影部分,已知菱形ABCD的边长为8cm,∠A=60°.$\widehat{BD}$是以A为圆心.AB为半径的弧.$\widehat{CD}$是以B为圆心.BC为半径的弧,求该商标图案的面积.
分析 连接BD,过点D作DE⊥BC,垂足为E,由四边形ABCD是菱形,∠A=60°可知△ABD及△BCD是等边三角形,故阴影部分的面积等于△BCD的面积,再求出DE的长,由三角形的面积公式即可得出结论.
解答 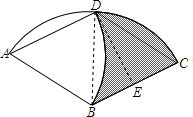 解:连接BD,过点D作DE⊥BC,垂足为E,
解:连接BD,过点D作DE⊥BC,垂足为E,
∵四边形ABCD是菱形,∠A=60°,
∴△ABD及△BCD是等边三角形,
∴S阴影=S△BCD=$\frac{1}{2}$BC•DE=$\frac{1}{2}$×8×8×sin60°=32×$\frac{\sqrt{3}}{2}$=16$\sqrt{3}$cm2.
答:该商标图案的面积为16$\sqrt{3}$cm2.
点评 本题考查的是扇形面积的计算及菱形的性质,根据题意作出辅助线,得出S阴影=S△BCD是解答此题的关键.

练习册系列答案
相关题目
 若点M为正方形ABCD边AB上任意一点,作DM=MN交∠ABC外角的平分线于点N,求∠DMN的度数.
若点M为正方形ABCD边AB上任意一点,作DM=MN交∠ABC外角的平分线于点N,求∠DMN的度数.
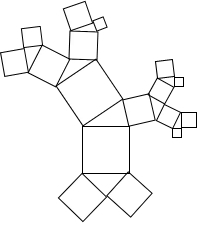 如图,美丽的珊瑚礁图案中,所有的四边形都是正方形,所有的三角形都是直角三角形.所有正方形(包括最大的正方形)的面积之和为500cm2,最大的正方形边长为10.
如图,美丽的珊瑚礁图案中,所有的四边形都是正方形,所有的三角形都是直角三角形.所有正方形(包括最大的正方形)的面积之和为500cm2,最大的正方形边长为10.
 观察图,先填空,然后回答问题:
观察图,先填空,然后回答问题: 如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列问题:
如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列问题: