题目内容
 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):| 项目 人员 | 阅读 | 思维 | 表达 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
考点:频数(率)分布直方图,算术平均数,加权平均数
专题:图表型
分析:(1)根据平均数的计算公式分别进行计算即可;
(2)根据加权平均数的计算公式分别进行解答即可;
(3)由直方图知成绩最高一组分数段85≤x<90中有7人,公司招聘8人,再根据x甲=85.5分,得出甲在该组,甲一定能被录用,在80≤x<85这一组内有10人,仅有1人能被录用,而x乙=84.8分,在这一段内不一定是最高分,得出乙不一定能被录用;最后根据频率=
进行计算,即可求出本次招聘人才的录用率.
(2)根据加权平均数的计算公式分别进行解答即可;
(3)由直方图知成绩最高一组分数段85≤x<90中有7人,公司招聘8人,再根据x甲=85.5分,得出甲在该组,甲一定能被录用,在80≤x<85这一组内有10人,仅有1人能被录用,而x乙=84.8分,在这一段内不一定是最高分,得出乙不一定能被录用;最后根据频率=
| 频数 |
| 总数 |
解答:解:(1)∵甲的平均成绩是:x甲=
=84(分),
乙的平均成绩为:x乙=
=85(分),
∴x乙>x甲,
∴乙将被录用;
(2)根据题意得:
x甲=
=85.5(分),
x乙=
=84.8(分);
∴x甲>x乙,
∴甲将被录用;
(3)甲一定被录用,而乙不一定能被录用,理由如下:
由直方图知成绩最高一组分数段85≤x<90中有7人,公司招聘8人,又因为x甲=85.5分,显然甲在该组,所以甲一定能被录用;
在80≤x<85这一组内有10人,仅有1人能被录用,而x乙=84.8分,在这一段内不一定是最高分,所以乙不一定能被录用;
由直方图知,应聘人数共有50人,录用人数为8人,
所以本次招聘人才的录用率为:
=16%.
| 93+86+73 |
| 3 |
乙的平均成绩为:x乙=
| 95+81+79 |
| 3 |
∴x乙>x甲,
∴乙将被录用;
(2)根据题意得:
x甲=
| 93×3+86×5+73×2 |
| 3+5+2 |
x乙=
| 95×3+81×5+79×2 |
| 3+5+2 |
∴x甲>x乙,
∴甲将被录用;
(3)甲一定被录用,而乙不一定能被录用,理由如下:
由直方图知成绩最高一组分数段85≤x<90中有7人,公司招聘8人,又因为x甲=85.5分,显然甲在该组,所以甲一定能被录用;
在80≤x<85这一组内有10人,仅有1人能被录用,而x乙=84.8分,在这一段内不一定是最高分,所以乙不一定能被录用;
由直方图知,应聘人数共有50人,录用人数为8人,
所以本次招聘人才的录用率为:
| 8 |
| 50 |
点评:此题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
相关题目
 钓鱼岛自古以来就是中国的领土.如图,我国甲、乙两艘海监执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往C处海域巡查的任务,并测得C处位于A处北偏东59°方向、位于B处北偏西44°方向.若甲、乙两船分别沿AC,BC方向航行,其平均速度分别是20海里/小时,18海里/小时,试估算哪艘船先赶到C处.
钓鱼岛自古以来就是中国的领土.如图,我国甲、乙两艘海监执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往C处海域巡查的任务,并测得C处位于A处北偏东59°方向、位于B处北偏西44°方向.若甲、乙两船分别沿AC,BC方向航行,其平均速度分别是20海里/小时,18海里/小时,试估算哪艘船先赶到C处.
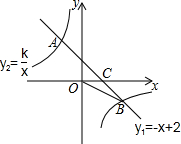 如图,一次函数y1=-x+2的图象与反比例函数y2=
如图,一次函数y1=-x+2的图象与反比例函数y2= 关于体育选考项目统计图
关于体育选考项目统计图