题目内容
13.在△ABC中,AB=AC=8,∠BAC=120°,BC=8$\sqrt{3}$,则S△ABC=16$\sqrt{3}$.分析 作AD⊥BC于D,根据等腰三角形的性质、三角形内角和定理得到∠B=30°,根据直角三角形的性质求出AD,根据三角形的面积公式计算即可.
解答 解: 作AD⊥BC于D,
作AD⊥BC于D,
∵AB=AC,∠BAC=120°,
∴∠B=30°,
∴AD=$\frac{1}{2}$AB=4,
∴S△ABC=$\frac{1}{2}$×BC×AD=16$\sqrt{3}$,
故答案为:16$\sqrt{3}$.
点评 本题考查的是直角三角形的性质,掌握直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
1.当a>0时,下列各式成立的是( )
| A. | a2=-a2 | B. | a2=(-a)2 | C. | a3=-a3 | D. | a3=(-a)3 |
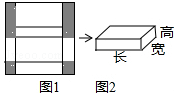 图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积.
图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积.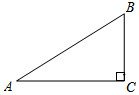 如图,在Rt△ABC中,∠C=90°,AB=10,tanA=$\frac{3}{4}$,则AC的长是8.
如图,在Rt△ABC中,∠C=90°,AB=10,tanA=$\frac{3}{4}$,则AC的长是8.