Question

14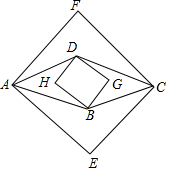．如图，菱形ABCD的面积为60cm²，则正方形AECF和正方形BGDH的面积之和的最小值为120cm²．

Answer 1

分析 设菱形的对角线长分别为2a，2b，则$\frac{1}{2}$•2a•2b=60，推出ab=30，因为正方形AECF和正方形BGDH的面积之和=（$\sqrt{2}$a）²+（$\sqrt{2}$b）²=2（a²+b²），因为（a-b）²≥0推出a²+b²≥2ab，推出2（a²+b²）≥4ab，推出2（a²+b²）≥120，所以正方形AECF和正方形BGDH的面积之和最小值为120cm²．

解答 解：设菱形的对角线长分别为2a，2b，则$\frac{1}{2}$•2a•2b=60，
∴ab=30，
∴正方形AECF和正方形BGDH的面积之和=（$\sqrt{2}$a）²+（$\sqrt{2}$b）²=2（a²+b²），
∵（a-b）²≥0
∴a²+b²≥2ab，
∴2（a²+b²）≥4ab，
∴2（a²+b²）≥120，
∴正方形AECF和正方形BGDH的面积之和最小值为120cm²．
故答案为120．

点评 本题考查菱形的性质、正方形的性质、完全平方公式等知识，解题的关键是学会利用参数，用转化的思想思考问题，属于中考填空题中的压轴题．