Question

8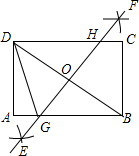．如图，在矩形ABCD中，用直尺和圆规作BD的垂直平分线EF，交AB于点G，交DC于点H，若AB=8，BC=6，则AG的长为$\frac{9}{8}$．

Answer 1

分析 由矩形的性质得出AD=BC=6，∠A=90°，由线段垂直平分线的性质得出DG=BG，设AG=x，则DG=BG=8-x，由勾股定理得出方程，解方程即可求出AG的长．

解答 解：∵四边形ABCD是矩形，
∴AD=BC=6，∠A=90°，
∵EF是BD的垂直平分线，
∴DG=BG，
设AG=x，则DG=BG=8-x，
在Rt△ADG中，由勾股定理得：AD²+AG²=DG²，
即6²+x²=（8-x）²，
解得：x=$\frac{7}{4}$；
即AG的长为$\frac{7}{4}$；
故答案为：$\frac{7}{4}$

点评 本题考查了矩形的性质、线段垂直平分线的性质、勾股定理；熟练掌握矩形的性质，由勾股定理得出方程是解决问题的关键．