题目内容
16.已知△ABC的两边BC=a,AC=b,且BC、AC边上的两条中线AD、BE互相垂直,则第三边AB的长用a、b来表示是$\frac{\sqrt{5{a}^{2}+5{b}^{2}}}{5}$.分析 连接DE,证明DE是△ABC的中位线,由三角形中位线定理得出由勾股定理得出AO2+EO2=AE2=$\frac{{b}^{2}}{4}$①,BO2+EO2=BD2=$\frac{{a}^{2}}{4}$②,①+②得出AO2+EO2+BO2+EO2=$\frac{{a}^{2}+{b}^{2}}{4}$,得出$\frac{5A{B}^{2}}{4}$=$\frac{{a}^{2}+{b}^{2}}{4}$,即可得出结果.
解答 解:连接DE,如图所示:
∵AD、BE是中线,
∴AE=$\frac{1}{2}$AC=$\frac{1}{2}$b,BD=$\frac{1}{2}$BC=$\frac{1}{2}$a,DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AB,
∵AD⊥BE,
∴∠AOE=∠AOB=∠BOD=∠DOE=90°,
由勾股定理得:AO2+EO2=AE2=$\frac{{b}^{2}}{4}$①,
BO2+EO2=BD2=$\frac{{a}^{2}}{4}$②,
①+②得:AO2+EO2+BO2+EO2=$\frac{{a}^{2}+{b}^{2}}{4}$,
即$A{B}^{2}+D{E}^{2}=\frac{{a}^{2}+{b}^{2}}{4}$,
∴$\frac{5A{B}^{2}}{4}$=$\frac{{a}^{2}+{b}^{2}}{4}$,
∴AB=$\frac{\sqrt{5{a}^{2}+5{b}^{2}}}{5}$;
故答案为:$\frac{\sqrt{5{a}^{2}+5{b}^{2}}}{5}$.
点评 本题考查了勾股定理、三角形中位线定理;熟练掌握勾股定理和三角形中位线定理,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
7.下列线段不能组成直角三角形的是( )
| A. | a=6,b=8,c=10 | B. | a=9,b=16,c=25 | C. | a=$\frac{4}{5}$,b=1,c=$\frac{3}{5}$ | D. | a=2,b=3,c2=13 |
1.下列公式正确的是( )
| A. | a2=b2+c2+2bccosA | B. | a2=b2+c2+bccosA | ||
| C. | a2=b2+c2-2bccosA | D. | a2=b2+c2-2bcsinA |
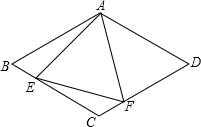 如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合. 如图,已知线段AC=12cm,在线段AC上有一点B,且BC=4cm,M是线段AC的中点,求线段MB的长.
如图,已知线段AC=12cm,在线段AC上有一点B,且BC=4cm,M是线段AC的中点,求线段MB的长.