题目内容
如图，一条公路修到湖边时，需拐弯绕湖而过；如果第一次拐的角∠A=96°，第二次拐的角∠B=136°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C=考点：平行线的性质
专题：应用题
分析：过点B作拐弯之前的道路的平行线，如图，根据平行线的性质由a∥b得∠1=∠A=96°，则∠2=40°，再根据平行线的性质得c∥b，所以∠C=180°-∠2=140°．
解答：
解：过点B作拐弯之前的道路的平行线，如图，
∵a∥b，
∴∠1=∠A=96°，
而∠B=∠1+∠2=136°，
∴∠2=136°-96°=40°，
∵a∥c，
∴c∥b，
∴∠2+∠C=180°，
∴∠C=180°-∠2=180°-40°=140°．
故答案为140°．
解：过点B作拐弯之前的道路的平行线，如图，∵a∥b，
∴∠1=∠A=96°，
而∠B=∠1+∠2=136°，
∴∠2=136°-96°=40°，
∵a∥c，
∴c∥b，
∴∠2+∠C=180°，
∴∠C=180°-∠2=180°-40°=140°．
故答案为140°．
点评：本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，方格纸中每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点在格点上． 且A（1，-2），B（5，-4），C（4，1）
如图，在?ABCD中，AC=6，BD=8，AC⊥BD，则AB的长为
如图，在菱形ABCD中，∠B=60°，点E，F分别从点B，D同时以同样的速度沿边BC，DC向点C运动．给出以下四个结论：
如图在平面直角坐标系上有点A（1，0），点A第一次跳动至点A1（-1，1），第四次向右跳动5个单位至点A4（3，2），…，依此规律跳动下去，点A第200次跳动至点A200的坐标是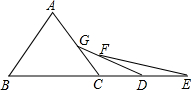
如图，已知△ABC中AB=AC，∠A=68°，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=