题目内容
如果?ABCD的对角线AC、BD相交于点O，△AOB的面积为4，那么?ABCD的面积为 ．
考点：平行四边形的性质
专题：
分析：因为平行四边形的对角线互相平分，所以平行四边形被对角线分成的四部分的面积相等，即?ABCD的面积=△AOB的面积×4．
解答：解：∵点O是平行四边形ABCD的对角线AC和BD的交点，
∴OA=OC，OB=OD，
在△AOB与△COD中，
，
∴△AOB≌△COD（SAS）．
同理，△BOC≌△DOA．
又AO是△ABD的中线，
∴△AOB与△AOD的面积相等，
故?ABCD的面积=△AOB的面积×4=4×4=16．
故答案是：16．
∴OA=OC，OB=OD，
在△AOB与△COD中，
|
∴△AOB≌△COD（SAS）．
同理，△BOC≌△DOA．
又AO是△ABD的中线，
∴△AOB与△AOD的面积相等，
故?ABCD的面积=△AOB的面积×4=4×4=16．
故答案是：16．
点评：本题考查了平行四边形的性质．解题时，充分利用了平行四边形的对角线互相平分的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为45m/min．在甲出发2min后，乙从A乘缆车到B，在B处停留1min后，再从B匀速步行到C．假设缆车匀速直线运动的速度为130m/min，山路AC长为1260m，经测量，cosA=
如图，在菱形ABCD中，∠B=60°，点E，F分别从点B，D同时以同样的速度沿边BC，DC向点C运动．给出以下四个结论：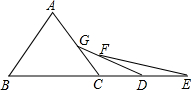
如图，已知△ABC中AB=AC，∠A=68°，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=
如图，OD⊥BC，垂足为D，BD=6厘米，OD=8厘米，OB=10厘米，那么点B到OD的距离为