��Ŀ����
����������һ���۵����
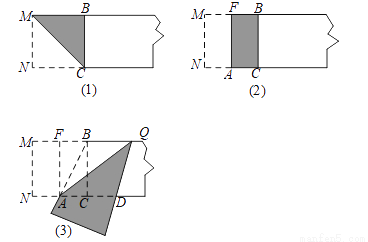
��һ������һ�ſ�Ϊ2�ľ���ֽƬ��һ�ˣ�����ͼ��1���ķ����۳�һ�������Σ�Ȼ���ֽƬչƽ���ۺ�ΪMC��
�ڶ�������ͼ��2����������������۳�������ȵľ��Σ��ٰ�ֽƬչƽ���ۺ�ΪFA��
���������۳��ڲ����FACB�ĶԽ���AB������AB�۵�ͼ��3������ʾ��AD�����ۺ�ΪAQ��
�������ϵIJ������̣�����������⣺
��1����CD�ij���
��2�����ж��ı���ABQD����״����˵��������ɣ�
��1������2���ı���ABQD�����Σ� �������������������1������֤���ı���MNCBΪ�����Σ�Ȼ���������۵������ʵõ���CA=1��AB=AD�����������CD=AD-AC��⼴�ɣ� ��2������ƽ���ߵ����ʺ��۵������ʿɵõ���BAQ=��BQA��Ȼ�����ݵȽǶԵȱߵ����ʵõ�AB=BQ��������������һ��Ա�ƽ������ȵ��ı���Ϊƽ���ı��ο�֤���ı���ABQD��ƽ���ı��Σ�����AB=AD���ɵ��ı�...
��ϰ��ϵ�д�
�����Ŀ


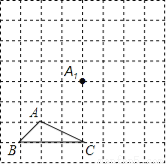
 ������ٶȴӵ�������ʧÿ��ɭ�ֵ���ʧ���ÿ�ѧ��������ʾӦΪ_____________���꣮
������ٶȴӵ�������ʧÿ��ɭ�ֵ���ʧ���ÿ�ѧ��������ʾӦΪ_____________���꣮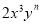 ��
��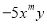 ��ͬ�����
��ͬ�����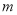 ��
�� 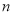 ��ֵΪ�� ��
��ֵΪ�� ��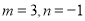
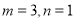
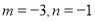
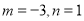 ��
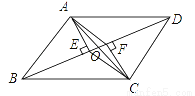
��
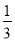 B. ��1 C. 2 D.
B. ��1 C. 2 D. 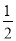
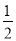 ,y=2.
,y=2.