题目内容
如图，已知AD是△ABC的边BC上的中线，△BME是△AMD绕点M按顺时针方向旋转180°得到的，连接AE，求证：DE=AC．考点：旋转的性质,平行四边形的判定与性质
专题：证明题
分析：若要证明DE=AC，则问题可转化为证明四边形AEDC是平行四边形即可．
解答：解：∵△BME是△AMD绕点M按顺时针方向旋转180°得到的，
∴△BME≌△AMD，
∴BE=AD，∠EBM=∠DAM，
∴BE∥AD，
∴四边形AEBD是平行四边形，
∴AE=BD，AE∥BD
∵BD=CD，
∴AE=CD，
∴四边形AEDC是平行四边形，
∴DE=AC．
∴△BME≌△AMD，
∴BE=AD，∠EBM=∠DAM，
∴BE∥AD，
∴四边形AEBD是平行四边形，
∴AE=BD，AE∥BD
∵BD=CD，
∴AE=CD，
∴四边形AEDC是平行四边形，
∴DE=AC．
点评：本题考查了旋转的性质以及平行四边形的判定和性质，题目的综合性较强，难度中等，是中考常见题型设计比较新颖．
练习册系列答案
相关题目
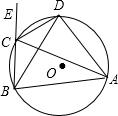如图，四边形ABCD内接于⊙O，E为BC延长线上一点，连接AC、BD，若DA=DB，求证：CD平分∠ACE．
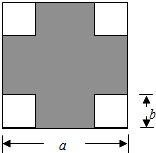如图，在一块边长为a的正方形纸板四角，各剪去一个边长为b（b＜
如图，正方形ABCD的边长为2，点E为AB的中点，以E为圆心，2为半径作圆，分别交AD、BC于M、N两点，与DC切于点P，求图中阴影部分的面积．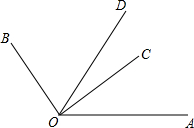
如图，∠BOC=2∠AOC，OD平分∠AOB，且∠COD=20°20′，求∠AOB的度数．
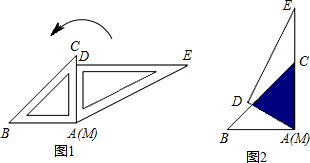将一副三角板按如图位置摆放，使得两块三角板的点A与M重合，点D在AC上．已知AB=AC=2
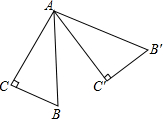如图，在Rt△ABC中，∠C=90°，∠B=60°，将△ABC绕点A逆时针旋转70°后得到△AB′C′，则∠CAB′=