题目内容
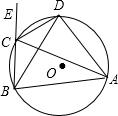 如图,四边形ABCD内接于⊙O,E为BC延长线上一点,连接AC、BD,若DA=DB,求证:CD平分∠ACE.
如图,四边形ABCD内接于⊙O,E为BC延长线上一点,连接AC、BD,若DA=DB,求证:CD平分∠ACE.考点:圆内接四边形的性质,圆周角定理
专题:证明题
分析:先根据圆内接四边形的性质得出∠DAB=∠DCE,再根据DA=DB得出∠DAB=∠DBA,故可得出∠DBA=∠DCE,再由圆周角定理得出∠DBA=∠DCA,故可得出∠DCA=∠DCE,故可得出结论.
解答:证明:∵四边形ABCD内接于⊙O,
∴∠DAB=∠DCE.
∵DA=DB,
∴∠DAB=∠DBA,
∴∠DBA=∠DCE.
∵∠DBA与∠DCA是同弧所对的圆周角,
∴∠DBA=∠DCA,
∴∠DCA=∠DCE,即CD平分∠ACE.
∴∠DAB=∠DCE.
∵DA=DB,
∴∠DAB=∠DBA,
∴∠DBA=∠DCE.
∵∠DBA与∠DCA是同弧所对的圆周角,
∴∠DBA=∠DCA,
∴∠DCA=∠DCE,即CD平分∠ACE.
点评:本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法中不正确的是( )
| A、-3.14既是负数,分数,也是有理数 |
| B、0既不是正数,也不是负数,但是整数 |
| C、-2000既是负数,也是整数,但不是有理数 |
| D、O是正数和负数的分界 |
 如图,线段AC、BD为四边形ABCD对角线.已知,∠ABC=∠ADC=90°,AD=DC,tan∠ACB=
如图,线段AC、BD为四边形ABCD对角线.已知,∠ABC=∠ADC=90°,AD=DC,tan∠ACB= 从图中能数出
从图中能数出 如图,已知AD是△ABC的边BC上的中线,△BME是△AMD绕点M按顺时针方向旋转180°得到的,连接AE,求证:DE=AC.
如图,已知AD是△ABC的边BC上的中线,△BME是△AMD绕点M按顺时针方向旋转180°得到的,连接AE,求证:DE=AC.