题目内容
过⊙O外一点P作⊙O的两条切线PA、PB,切线分别为A、B,C为圆周上除切点A、B外的任一点,若∠APB=70°,则∠ACB= .
考点:切线的性质
专题:
分析:连接OA、OB,根据切线的性质求出∠OAP=∠OBP=90°,求出∠AOB的度数,再根据圆周角定理求出即可.
解答: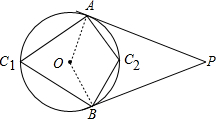 解:连接OA、OB,
解:连接OA、OB,
∵过⊙O外一点P作⊙O的两条切线PA、PB,切线分别为A、B,
∴∠OAP=∠OBP=90°,
∵∠APB=70°,
∴∠AOB=360°-90°-90°-70°=110°,
∴点C在C1上,∠ACB=
∠AOB=55°,
点C在C2上,∠ACB=180°-55°=125°,
故答案为:55°或125°.
 解:连接OA、OB,
解:连接OA、OB,∵过⊙O外一点P作⊙O的两条切线PA、PB,切线分别为A、B,
∴∠OAP=∠OBP=90°,
∵∠APB=70°,
∴∠AOB=360°-90°-90°-70°=110°,
∴点C在C1上,∠ACB=
| 1 |
| 2 |
点C在C2上,∠ACB=180°-55°=125°,
故答案为:55°或125°.
点评:本题考查了切线的性质,圆周角定理,圆内接四边形的性质的应用,解此题的关键是求出∠AOB的度数,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
下列说法中,正确的是( )
A、开不尽的平方根和立方根,如
| |||||
B、不可约分数,如
| |||||
| C、无理数是指开不尽的方根(平方根,立方根等) | |||||
| D、数轴上的每一个点都有一个有理数和它对应 |
 如图,已知Rt△ABC中,∠ACB=90°,AC=3,BC=6.绕点C旋转A′B′经过BC中点E,求B′E.
如图,已知Rt△ABC中,∠ACB=90°,AC=3,BC=6.绕点C旋转A′B′经过BC中点E,求B′E. 如图,△ABC的AB边和AC边上各取一点D和E,且使AD=AE,DE延长线与BC延长线相交于F,求证:
如图,△ABC的AB边和AC边上各取一点D和E,且使AD=AE,DE延长线与BC延长线相交于F,求证: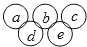 ,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如:
,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如: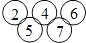 .
. .
.