题目内容
在奥运五环图案内,分别填写五个数a,b,c,d,e,如图,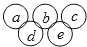 ,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如:
,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如: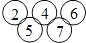 .
.
(1)请你在0~20之间选择另一组符合条件的数填入图中: .
.
(2)请你用n(n为自然数)表示三个连续偶数为 , , ;它们的和为 ;用m(m为自然数)表示两个连续奇数为 , ;它们的和为 ;
(3)对于任选的三个连续偶数,是否都存在两个连续奇数满足上述的填数方法.若存在请说明填数的方法;若不存在,则三个连续偶数正中间的数满足什么条件时一定存在.
 ,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如:
,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如: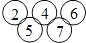 .
.(1)请你在0~20之间选择另一组符合条件的数填入图中:
 .
.(2)请你用n(n为自然数)表示三个连续偶数为
(3)对于任选的三个连续偶数,是否都存在两个连续奇数满足上述的填数方法.若存在请说明填数的方法;若不存在,则三个连续偶数正中间的数满足什么条件时一定存在.
考点:规律型:数字的变化类
专题:
分析:(1)要求三个连续偶数之和等于两个连续奇数之和且都在0到20之间,只需使两个奇数的和为3的倍数即可,据此可得出答案;
(2)由连续偶数之间相差2可用n(n为自然数)表示三个连续偶数,再求出它们的和;由连续奇数之间相差2可用用m(m为自然数)表示两个连续奇数,再求出它们的和;
(3)举出反例说明对于任选的三个连续偶数,不都存在两个连续奇数满足上述的填数方法;填数的方法是三个连续偶数正中间的数为4的倍数.根据a,b,c为三个连续偶数,且a+b+c=d+e,得到3b=d+e,根据d与e为两个连续的奇数,所以得到3b为6的倍数,d与e之间的偶数为6的倍数,三个连续偶数正中间的数为4的倍数.
(2)由连续偶数之间相差2可用n(n为自然数)表示三个连续偶数,再求出它们的和;由连续奇数之间相差2可用用m(m为自然数)表示两个连续奇数,再求出它们的和;
(3)举出反例说明对于任选的三个连续偶数,不都存在两个连续奇数满足上述的填数方法;填数的方法是三个连续偶数正中间的数为4的倍数.根据a,b,c为三个连续偶数,且a+b+c=d+e,得到3b=d+e,根据d与e为两个连续的奇数,所以得到3b为6的倍数,d与e之间的偶数为6的倍数,三个连续偶数正中间的数为4的倍数.
解答:解:(1)∵三个连续偶数之和等于两个连续奇数之和且都在0到20之间,
∴只需使两个奇数的和为3的倍数即可,
∴符合条件的数可以为 或
或 ;
;
(2)用n(n为自然数)表示三个连续偶数为2n-2,2n,2n+2;它们的和为6n;用m(m为自然数)表示两个连续奇数为2m-1,2m+1;它们的和为4m;
(3)对于任选的三个连续偶数,不都存在两个连续奇数满足上述的填数方法.例如:a=4,b=6,c=8时,a+b+c=18,则d+e=18,找不到两个连续奇数d与e的和为18;
填数的方法是三个连续偶数正中间的数为4的倍数,理由如下:
∵a,b,c为三个连续偶数,且a+b+c=d+e,
∴3b=d+e,
∵d与e为两个连续的奇数,
∴3b为6的倍数,
∴d与e之间的偶数为6的倍数,
∴三个连续偶数正中间的数为4的倍数.
故答案为2n-2,2n,2n+2;6n;2m-1,2m+1;4m.
∴只需使两个奇数的和为3的倍数即可,
∴符合条件的数可以为
 或
或 ;
;(2)用n(n为自然数)表示三个连续偶数为2n-2,2n,2n+2;它们的和为6n;用m(m为自然数)表示两个连续奇数为2m-1,2m+1;它们的和为4m;
(3)对于任选的三个连续偶数,不都存在两个连续奇数满足上述的填数方法.例如:a=4,b=6,c=8时,a+b+c=18,则d+e=18,找不到两个连续奇数d与e的和为18;
填数的方法是三个连续偶数正中间的数为4的倍数,理由如下:
∵a,b,c为三个连续偶数,且a+b+c=d+e,
∴3b=d+e,
∵d与e为两个连续的奇数,
∴3b为6的倍数,
∴d与e之间的偶数为6的倍数,
∴三个连续偶数正中间的数为4的倍数.
故答案为2n-2,2n,2n+2;6n;2m-1,2m+1;4m.
点评:考查了规律型:数字的变化类,解此题的关键是理解连续奇数和连续偶数的含义,突破点是满足三个连续偶数之和等于两个连续奇数之和.

练习册系列答案
相关题目
下列说法正确的是( )
| A、在墙上固定一根木条,至少需要2颗钉子 |
| B、射线OA和射线AO是同一条射线 |
| C、延长直线AB |
| D、线段AB和线段BA不是同一条线段 |
 已知AB=10cm,点C是线段AB上的一个动点,点D是线段AC的中点,点E是线段BC上一点,DE=5cm.
已知AB=10cm,点C是线段AB上的一个动点,点D是线段AC的中点,点E是线段BC上一点,DE=5cm. 如图,若把△ABC绕A点顺时针旋转一定角度,就得到△ADE,请写出图中所有的对应边是
如图,若把△ABC绕A点顺时针旋转一定角度,就得到△ADE,请写出图中所有的对应边是 如图,正方形ABCD的边长为4,以BC为直径的⊙O交对角线BD于C,过A点作⊙O的切线,交CD于E,切点为F,连接BF.
如图,正方形ABCD的边长为4,以BC为直径的⊙O交对角线BD于C,过A点作⊙O的切线,交CD于E,切点为F,连接BF. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为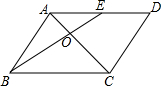 如图,在平行四边形ABCD中,点E为边AD的中点,连接AC、BE交于点O,若AO=3,则AC=
如图,在平行四边形ABCD中,点E为边AD的中点,连接AC、BE交于点O,若AO=3,则AC=