题目内容
8.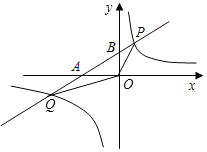 如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=$\frac{1}{2}$.
如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=$\frac{1}{2}$.(1)一次函数的解析式和反比例函数的解析式;
(2)求△POQ的面积.
分析 (1)作PM⊥x轴于点M.则∠POM=90°-∠BOP=45°,△OPM是等腰直角三角形.首先求得B的坐标,然后根据三角函数的定义求得OB的长,在直角△PAM中利用三角函数求得P的坐标,然后利用待定系数法求得一次函数以及反比例函数的解析式;
(2)解两个函数解析式组成的方程组求得Q的坐标,然后利用三角形面积公式求得三角形的面积.
解答 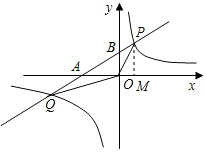 解:(1)作PM⊥x轴于点M.则∠POM=90°-∠BOP=45°,△OPM是等腰直角三角形.
解:(1)作PM⊥x轴于点M.则∠POM=90°-∠BOP=45°,△OPM是等腰直角三角形.
在y=kx+1中令x=0,则y=1,即B的坐标是(0,1),OB=1.
∵tan∠BAO=$\frac{OB}{OA}$=$\frac{1}{2}$,
∴OA=2.
即设PM=m,则OM=PM=x.
在直角△APM中,AM=2+x,tan∠PAM=$\frac{x}{x+2}$=$\frac{1}{2}$,
解得x=2,
则P的坐标是(2,2).
把(2,2)代入y=kx+1得2=2k+1,解得k=$\frac{1}{2}$,则一次函数的解析式是y=$\frac{1}{2}$x+1.
设反比例函数的解析式是y=$\frac{n}{x}$,把(2,2)代入得n=4,则反比例函数的解析式是y=$\frac{4}{x}$;
(2)根据题意得$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=\frac{4}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-1}\end{array}\right.$,
则Q的坐标是(-4,-1).
则S△POQ=$\frac{1}{2}$×1×(2+4)=3.
点评 本题考查了待定系数法求函数解析式,以及三角函数的定义,求得P的坐标是解决本题的关键.

| A. | 若a>b,则a+c>b+c | B. | 若a+c>b+c,则a>b | C. | 若a>b,则ac2>bc2 | D. | 若a>b,则1+a>b-1 |
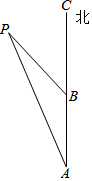 如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.
如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.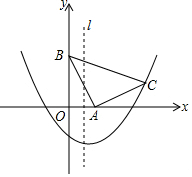 如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=$\frac{1}{2}$x2+bx-2的图象过C点.
如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=$\frac{1}{2}$x2+bx-2的图象过C点.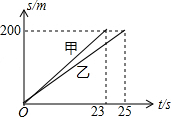 如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:
如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题: 观察图,先填空,然后回答问题.
观察图,先填空,然后回答问题.