题目内容
如果一个函数的自变量只取整数,那么其函数的图象是“一群孤立的点”这样的函数我们称为离散型函数.已知离散型函数y=x2-2mx+3(x为整数),当x≤6时,y随x的增大而增大,则m的取值范围是 .
考点:二次函数的性质
专题:新定义
分析:先由x≤6时,y随x的增大而增大,可设x1<x2≤6,则x12-2mx1+3<x22-2mx2+3,再根据不等式的性质即可求出m的取值范围.
解答:解:∵x≤6时,y随x的增大而增大,
∴设x1<x2≤6,则x12-2mx1+3<x22-2mx2+3,
∴x12-x22<2mx1-2mx2,
(x1-x2)(x1+x2)<2m(x1-x2),
∵x1-x2<0,
∴x1+x2>2m,
∵x2最大值取6,x1最大值取5,
∴x1+x2≤11,即2m<11,
∴m<
.
故答案为m<
.
∴设x1<x2≤6,则x12-2mx1+3<x22-2mx2+3,
∴x12-x22<2mx1-2mx2,
(x1-x2)(x1+x2)<2m(x1-x2),
∵x1-x2<0,
∴x1+x2>2m,
∵x2最大值取6,x1最大值取5,
∴x1+x2≤11,即2m<11,
∴m<
| 11 |
| 2 |
故答案为m<
| 11 |
| 2 |
点评:本题考查了二次函数的性质,不等式的性质,难度适中.透彻理解题意是解题的关键.

练习册系列答案
相关题目
 如图,正方形的边长为a,剪去四个角后成为一个正八边形,则这个正八边形的边长为
如图,正方形的边长为a,剪去四个角后成为一个正八边形,则这个正八边形的边长为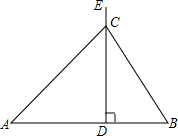 如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与D不重合),分别联结CA、CB,得到△ABC.
如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与D不重合),分别联结CA、CB,得到△ABC.