Question

10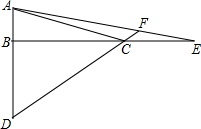．如图．在△ABC中，∠ABC=90°，点D、E分别在AB、BC的延长线上，且AD=BC，延长DC交AE于F，∠AFD=45°．求证：BD=CE．

Answer 1

分析 如图过点A作AF⊥AB，并截取AF=BD，连接DF、CF，证明四边形AFCE为平行四边形，得AF=CE即可解决问题．

解答 证明：如图过点A作AF⊥AB，并截取AF=BD，连接DF、CF，

∵∠ABC=90°，AF⊥AB，
∴∠FAD=∠DBC=90°
在△ADF和△BCD中，
$\left\{\begin{array}{l}{AD=BC}\\{∠FAD=∠DBC=90°}\\{AF=BD}\end{array}\right.$
∴△ADF≌△BCD，
∴DF=DC，∠ADF=∠BCD，
∵∠BCD+∠BDC=90°，
∴∠ADF+∠BDC=90°，
∴∠FDC=90°，
∴∠FCD=∠DFC=45°=∠APD，
∴FC∥AE，∵AF∥CE，
∴四边形AFCE是平行四边形，
∴AF=CE=BD，
∴BD=CE．

点评 本题考查了全等三角形的性质与判定、平行四边形的判定和性质、等腰直角三角形的判定和性质等知识，解决本题的关键是作出辅助线，得出四边形AFCE为平行四边形．