题目内容
15.一名同学在计算某个样本的方差时用到了以下算式:S2=$\frac{1}{a}$[3(x1-4)2+2(x2-4)2+5(x3-4)2+2(x4-4)2+3(x5-4)2].
(1)这组样本数据的平均数是多少?
(2)a在这个样本中表示什么?试求出a的值.
(3)若x1=2,x2=3,x3=4,x4=5,试求出x5的值.
分析 (1)(2)方差的计算公式:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],其中n是这个样本的容量,$\overline{x}$是样本的平均数,由此就可得到答案;
(3)根据这组样本数据的平均数是4即可求出x5的值.
解答 解:(1)∵S2=$\frac{1}{a}$[3(x1-4)2+2(x2-4)2+5(x3-4)2+2(x4-4)2+3(x5-4)2],
∴这组样本数据的平均数是4;
(2)a在这个样本中表示样本容量.
a=3+2+5+2+3=15;
(3)∵x1=2,x2=3,x3=4,x4=5,
∴3×2+2×3+5×4+2×5+3x5=4×15,
∴x5=6.
点评 本题考查方差的定义:一般地,设n个数据x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],理解方差计算公式中各个字母的含义是解题的关键.

练习册系列答案
相关题目
3.国家气象局监测2015年某日24小时PM2.5的值,其中6个时刻的数值如表:
则这组数据的中位数和平均数分别是( )
| 时刻 | 4时 | 5时 | 6时 | 7时 | 8时 | 9时 |
| PM2.5(毫克∕立方米) | 342 | 342 | 333 | 329 | 325 | 324 |
| A. | 331;332.5 | B. | 329;332.5 | C. | 331;332 | D. | 333;332 |
 如图,BC是⊙O的直径,BF是弦,AD过圆心O,AD⊥BF,AE⊥BC于E,连接DE、FC.
如图,BC是⊙O的直径,BF是弦,AD过圆心O,AD⊥BF,AE⊥BC于E,连接DE、FC.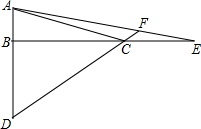 如图.在△ABC中,∠ABC=90°,点D、E分别在AB、BC的延长线上,且AD=BC,延长DC交AE于F,∠AFD=45°.求证:BD=CE.
如图.在△ABC中,∠ABC=90°,点D、E分别在AB、BC的延长线上,且AD=BC,延长DC交AE于F,∠AFD=45°.求证:BD=CE.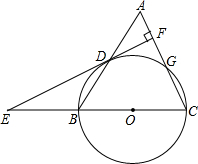 如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.
如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.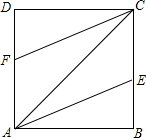 如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.