题目内容
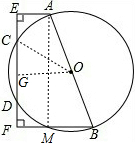
 如图,AB是⊙O的直径,CD是弦,AE⊥CD,BF⊥CD,AB=10,AE=3,BF=5,求CE的长.
如图,AB是⊙O的直径,CD是弦,AE⊥CD,BF⊥CD,AB=10,AE=3,BF=5,求CE的长.考点:垂径定理,勾股定理,梯形中位线定理
专题:
分析:过点O作OG⊥CD于点G,连接OG,由垂径定理可知CG=
CD,根据点O是AB的中点可知OG是梯形AEFB的中位线,故可得出OG的长,根据勾股定理可得出CG的长,根据勾股定理求出AM长,进而得出结论.
| 1 |
| 2 |
解答:解:过点O作OG⊥CD于点G,连接OG,过A作AM⊥BF于M,
∵AE⊥CD,BF⊥CD,
∴∠E=∠F=∠AMF=90°,
∴四边形AEFM是矩形,
∴AE=FM=3,EF=AM,∠AMF=∠AMB=90°,
∴BM=5-3=2,
由勾股定理得:EF=AM=
=4
,
∵点O是圆心,
∴CG=
CD.
∵点O是AB的中点,AE⊥CD于E,BF⊥CD于F,
∴OG是梯形AEFB的中位线,
∵AE=3,BF=5,
∴OG=
=4.
在Rt△OCG中,
∵OG=4cm,OC=5cm,
∴CG=
=
=3,
∴CE=
×4
-3=2
-3.

∵AE⊥CD,BF⊥CD,
∴∠E=∠F=∠AMF=90°,
∴四边形AEFM是矩形,
∴AE=FM=3,EF=AM,∠AMF=∠AMB=90°,
∴BM=5-3=2,
由勾股定理得:EF=AM=
| 102-22 |
| 6 |
∵点O是圆心,
∴CG=
| 1 |
| 2 |
∵点O是AB的中点,AE⊥CD于E,BF⊥CD于F,
∴OG是梯形AEFB的中位线,
∵AE=3,BF=5,
∴OG=
| 3+5 |
| 2 |
在Rt△OCG中,
∵OG=4cm,OC=5cm,
∴CG=
| OC2-OG2 |
| 52-42 |
∴CE=
| 1 |
| 2 |
| 6 |
| 6 |
点评:本题考查的是垂径定理,勾股定理,矩形的性质和判定的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目