题目内容
11. 如图,已知A(2$\sqrt{3}$,2),B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转90°,得到△A′OB′,则图中阴影部分的面积为$\frac{3}{4}π$.
如图,已知A(2$\sqrt{3}$,2),B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转90°,得到△A′OB′,则图中阴影部分的面积为$\frac{3}{4}π$.
分析 根据旋转的性质可知阴影部分的面积=S扇形A′OA-S扇形B′OB,根据扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$计算即可.
解答 解:∵点A的坐标为(2$\sqrt{3}$,2),
∴OA=4,
∵点B的坐标为(2$\sqrt{3}$,1),
∴OB=$\sqrt{13}$,
由旋转的性质可知,S△A′OB′=S△AOB,
∴阴影部分的面积=S扇形A′OA-S扇形B′OB
=$\frac{90π×16}{360}$-$\frac{90π×13}{360}$
=$\frac{3}{4}π$,
故答案为:$\frac{3}{4}π$.
点评 本题考查的是扇形的面积计算和旋转的性质,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$、正确根据旋转的性质表示出阴影部分的面积是解题的关键.

练习册系列答案
相关题目
6.下列图形中,是中心对称图形的为( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.空调常使用的三种制冷剂的沸点如下表所示,那么这三种制冷剂按沸点从低到高排列的顺序是( )
| 制冷剂编号 | R22 | R12 | R410A |
| 制冷剂 | 二氟一氯甲烷 | 二氟二氯甲烷 | 二氟甲烷50%,五氟乙烷50% |
| 沸点近似值 (精确到1℃) | -41 | -30 | -52 |
| A. | R12,R22,R410A | B. | R22,R12,R410A | C. | R410A,R12,R22 | D. | R410A,R22,R12 |
 如图,已知大长方形ACFH的面积为572,被分割成六个小正方形,设最小的正方形边长a,第二小的正方形边长为b.
如图,已知大长方形ACFH的面积为572,被分割成六个小正方形,设最小的正方形边长a,第二小的正方形边长为b. 如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是( )
如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是( )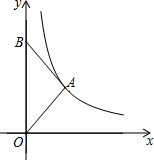 如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=$\frac{k}{x}({x>0})$的图象经过点A,若△ABO的面积为2,则k的值为2.
如图,在平面直角坐标系xOy中,点B在y轴上,AB=AO,反比例函数y=$\frac{k}{x}({x>0})$的图象经过点A,若△ABO的面积为2,则k的值为2.