题目内容
18.直角坐标系内有两点A(0,3)、B(2,-3),若P为x轴上一点,当△PAB为等腰三角形时,求点P的坐标.分析 分三种情况:①当AB=AP,即AB2=AP2,求得x=±$\sqrt{31}$;②当AP=BP,即AP2=BP2,求得x=1,则P是AB的中点,不合题意舍去;③当AB=BP,即AB2=BP2,求得x=2$±2\sqrt{19}$;于是得到符合题意的点P有四个.
解答 解:∵A(0,3),B(2,-3),
∴AB2=40,
设P(x,0).
∴AP2=9+x2,PB2=(x-2)2+9,
∵△PAB为等腰三角形,
∴分三种情况;
①当AB=AP,即AB2=AP2,
∴9+x2=40,解得:x=±$\sqrt{31}$,
②当AP=BP,即AP2=BP2,
∴9+x2=(x-2)2+9,
解得;x=1,则P是AB的中点,不合题意舍去;
③当AB=BP,即AB2=BP2,
∴40=(x-2)2+9,
解得:x=2$±2\sqrt{19}$,
∴点P的坐标为:($\sqrt{31}$,0),(-$\sqrt{31}$,0),(2+2$\sqrt{19}$,0)(2-2$\sqrt{19}$,0).
点评 本题考查了点的坐标的求法,综合运用了解直角三角形的知识,同时考查了根据特殊三角形的性质求三角形的顶点坐标的能力.

练习册系列答案
相关题目
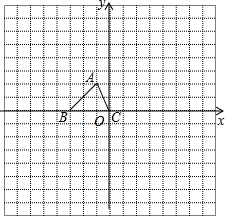 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).
如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).