题目内容
13.若x,y,z满足关系式|4x-4y+1|+$\frac{1}{5}$$\sqrt{2y+z}$+(z-$\frac{1}{2}$)2=0,求x2(y-z)的值.分析 利用非负数的性质列出方程组,求出方程组的解得到x,y,z的值,代入原式计算即可得到结果.
解答 解:∵|4x-4y+1|+$\frac{1}{5}$$\sqrt{2y+z}$+(z-$\frac{1}{2}$)2=0,
∴$\left\{\begin{array}{l}{4x-4y+1=0}\\{2y+z=0}\\{z-\frac{1}{2}=0}\end{array}\right.$,
解得:x=-$\frac{1}{2}$,y=-$\frac{1}{4}$,z=$\frac{1}{2}$,
则原式=$\frac{1}{4}$×(-$\frac{1}{4}$-$\frac{1}{2}$)=-$\frac{3}{16}$.
点评 此题考查了解三元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.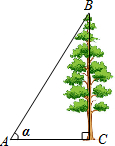 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )| A. | 6sin75°米 | B. | $\frac{6}{cos75°}$米 | C. | $\frac{6}{tan75°}$米 | D. | 6tan75°米 |
5.在菱形ABCD中,如果∠A:∠D=1:5,菱形的高是2cm,那么下列说法中,正确的是( )
| A. | 菱形的周长是8cm | B. | 菱形的面积是4cm2 | ||
| C. | 菱形的周长是10cm | D. | 菱形的面积是8cm2 |
 如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?
如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少? 如图,数轴的单位长度为1,如果R表示的数是-1,则数轴上表示相反数的两点是P,Q.
如图,数轴的单位长度为1,如果R表示的数是-1,则数轴上表示相反数的两点是P,Q.