Question

1．如图，在平面直角坐标系xOy中，抛物线y=ax²-8ax+b交y轴于点A（0，-1），抛物线最高点的纵坐标为$\frac{13}{3}$．
（1）求抛物线的解析式；
（2）点B在第一象限内的抛物线上，其横坐标为t（t≤4），BC⊥x轴于点C，点D在线段OC的延长线上，BD=AD，当CD=1时，求t的值；
（3）在（2）的条件下，点E在第一象限对称轴右侧的抛物线上，直线CE交y轴于点F，直线DE交y轴于点G，当EC•ED=CF•DG时，求点E的坐标．

Answer 1

分析 （1）将x=0代入可求得b的值，然后依据配方法将函数关系式变形为y=a（x-4）²-16a-1，最后依据顶点纵坐标为$\frac{13}{3}$可求得a的值，从而可求得抛物线的解析式；
（2）先根据题意画出图形，设点B的坐标为（t，-$\frac{1}{3}$t²+$\frac{8}{3}$t-1），则点D（t+1，0）．然后依据HL可证明Rt△OAD≌Rt△CDB，从而得到OD=BC，然后由OD=BC列出关于t的方程，于是可求得t的值；
（3）过点G作GM∥x轴，过点E作EM∥y轴，过点C作CH∥y轴，过点D作DI∥y轴．依据平行线分线段成立比例定理可得到：MH：GH=GI：IM．设点E的横坐标为x．然后依据C、D两点的坐标可求得GH、GI、HM、IM的长，然后依据比例关系列方程求解即可．

解答 解：（1）∵将x=0代入得：b=-1，
∴抛物线的解析式为y=ax²-8ax-1．
∴y=a（x²-8x+16-16）-1=a（x-4）²-16a-1．
∵抛物线最高点的纵坐标为$\frac{13}{3}$，
∴-16a-1=$\frac{13}{3}$．
解得：a=-$\frac{1}{3}$．
∴抛物线的解析式为y=-$\frac{1}{3}$x²+$\frac{8}{3}$x-1．
（2）如图1所示：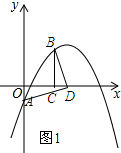

设点B的坐标为（t，-$\frac{1}{3}$t²+$\frac{8}{3}$t-1），则点D（t+1，0）．
在Rt△OAD和Rt△CDB中$\left\{\begin{array}{l}{OA=CD=1}\\{BD=AD}\end{array}\right.$，
∴Rt△OAD≌Rt△CDB．
∴OD=BC，即t+1=-$\frac{1}{3}$t²+$\frac{8}{3}$t-1，整理得：t²-5t+6=0，解得t=2或t=3．
∴t的值为2或3．
（3）如图2所示：过点G作GM∥x轴，过点E作EM∥y轴，过点C作CH∥y轴，过点D作DI∥y轴．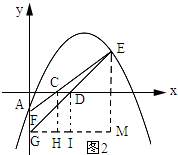

∵EC•ED=CF•DG，
∴CE：FC=DG：ED．
∵AG∥CH∥DI∥EM，
∴EC：CF=MH：GH，DG：ED=GI：IM．
∴MH：GH=GI：IM．
设点E的横坐标为x．
当C（2，0）、D（3，0）时，则MH=x-2，GH=2，GI=3，MI=x-3．
∵MH：GH=GI：IM，
∴$\frac{x-2}{2}$=$\frac{3}{x-3}$，整理得：x²-5x=0，解得：x=5或x=0（舍去）．
∵将x=5代入抛物线的解析式得y=-$\frac{1}{3}$×25+$\frac{8}{3}$×5-1=4，
∴E（5，4）．
当C（3，0）、D（4，0）时，则MH=x-3，GH=3，GI=4，MI=x-4．
∵MH：GH=GI：IM，
∴$\frac{x-3}{3}$=$\frac{4}{x-4}$，整理得：x²-7x=0，解得：x=7或x=0（舍去）．
∵将x=7代入抛物线的解析式得y=-$\frac{1}{3}$×49+$\frac{8}{3}$×7-1=$\frac{4}{3}$，
∴E（7，$\frac{4}{3}$）．
综上述所，点E的坐标为（5，4）或（7，$\frac{4}{3}$）．

点评 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、全等三角形的性质和判定、平行线分线段成比例定理的应用，依据平行线分线段成比例得到MH：GH=GI：IM是解题的关键．