题目内容
1. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为x>-1.
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为x>-1.
分析 求关于x的不等式k1x+b>k2x的解集就是求:能使函数y=k1x+b的图象在函数y=k2x的上边的自变量的取值范围.
解答 解:能使函数y=k1x+b的图象在函数y=k2x的上边时的自变量的取值范围是x>-1.
故关于x的不等式k1x+b>k2x的解集为:x>-1.
故答案为:x>-1.
点评 本题考查了一次函数与一元一次不等式的关系,从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.利用数形结合是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
12.$\sqrt{\frac{1}{16}}$的平方根是( )
| A. | ±$\frac{1}{2}$ | B. | ±$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
9.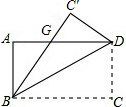 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )| A. | 18.75cm2 | B. | 19.15cm2 | C. | 20cm2 | D. | 21.35cm2 |
13.下列运算正确的是( )
| A. | 2$\sqrt{2}×\sqrt{2}=4$ | B. | 2a3•a4=2a7 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |




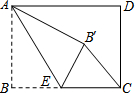 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,把∠B沿AE折叠,使点B落在点B′处,则:①AB′=3;②当△CEB′为直角三角形时,BE=3或$\frac{3}{2}$.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,把∠B沿AE折叠,使点B落在点B′处,则:①AB′=3;②当△CEB′为直角三角形时,BE=3或$\frac{3}{2}$.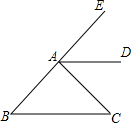 如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.
如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.