题目内容
2. 如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(点D不与点A、B重合),连接CD,过点D作CD的垂线交射线CA于点E.当△ADE为等腰三角形时,AD的长度为1或$\sqrt{3}$.
如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(点D不与点A、B重合),连接CD,过点D作CD的垂线交射线CA于点E.当△ADE为等腰三角形时,AD的长度为1或$\sqrt{3}$.
分析 分两种情况:①当点E在AC上时,AE=AD,则∠EDA=∠BAC=30°,由含30°角的直角三角形的性质得出BC=$\frac{1}{2}$AB=1,∠B=60°,得出AC=$\sqrt{3}$,∠BCD=60°,证出△BCD是等边三角形,得出CD=BC=1,AD=CD=1;
②当点E在射线CA上时,AE=AD,得出∠E=∠ADE=15°,由三角形内角和定理得出∠ACD=∠CDA,由等角对等边得出AD=AC=$\sqrt{3}$;即可得出结果.
解答 解:分两种情况:①当点E在AC上时,AE=AD,
∴∠EDA=∠BAC=30°,
∵DE⊥CD,
∴∠BDC=60°,
∵∠ACB=90°,∠BAC=30°,
∴BC=$\frac{1}{2}$AB=1,∠B=60°,
∴AC=$\sqrt{3}$,∠BCD=60°,
∴△BCD是等边三角形,∠DCA=30°=∠BAC,
∴CD=BC=1,AD=CD=1;
②当点E在射线CA上时,如图所示:
AE=AD,
∴∠E=∠ADE=15°,
∵DE⊥CD,
∴∠CDA=90°-15°=75°,
∴∠ACD=180°-30°-75°=75°=∠CDA,
∴AD=AC=$\sqrt{3}$;
综上所述:AD的长度为1或$\sqrt{3}$;
故答案为:1或$\sqrt{3}$.
点评 本题考查了勾股定理、等腰三角形的判定与性质、含30°角的直角三角形的性质、等边三角形的判定与性质等知识;熟练掌握等腰三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
12.关于一次函数y=2x-1,y=-2x+1的图象,下列说法正确的是( )
| A. | 关于直线y=-x对称 | B. | 关于x轴对称 | ||
| C. | 关于y轴对称 | D. | 关于直线y=x对称 |
 已知线段a,b,c,求作:线段m,使m=a-b+c.
已知线段a,b,c,求作:线段m,使m=a-b+c. 如图,l1∥l2,AB∥CD,BC=2CF.若△CEF的面积是5,求四边形ABCD的面积.
如图,l1∥l2,AB∥CD,BC=2CF.若△CEF的面积是5,求四边形ABCD的面积.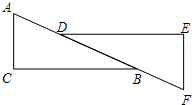 如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.
如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE. 如图,△ABC中,BD⊥AC于D,CE⊥AB于E,BD=CE.求证:△ABC是等腰三角形.
如图,△ABC中,BD⊥AC于D,CE⊥AB于E,BD=CE.求证:△ABC是等腰三角形. 已知正六边形的边长为4cm,分别以它的三个不相邻的顶点为圆心,边长为半径画弧(如图),则所得到的三条弧的长度之和为8πcm.(结果保留π)
已知正六边形的边长为4cm,分别以它的三个不相邻的顶点为圆心,边长为半径画弧(如图),则所得到的三条弧的长度之和为8πcm.(结果保留π)