题目内容
如图,正方形ABCD和正方形AEFG有公共的顶点A,连BG、DE,M为DE的中点,连AM.
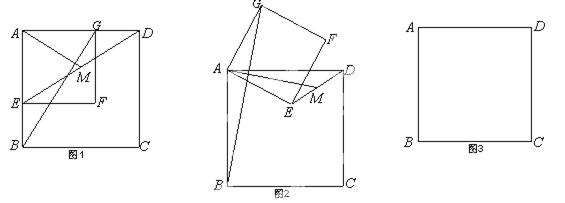
(1)如图1,AE、AG分别与AB、AD重合时,AM和BG的大小和位置关系分别是 、_ ____;
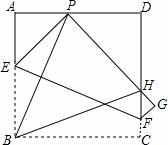
(2)将图1中的正方形AEFG绕A点旋转到如图2,则(1)中的结论是否仍成立?试证明你的结论;
(3)若将图1中的正方形AEFG绕A点逆时针旋转到正方形ABCD外时,则AM和BG的大小和位置关系分别是__________、____________,请你在图3中画出图形,并直 接写出结论,不要求证明.
接写出结论,不要求证明.
(1)BG=2AM,AM⊥BG;
(2)成立,证明见解析;
(3)如图所示,BG=2AM,AM⊥BG,画图见解析;
【解析】(1)BG=2AM,AM⊥BG;
(2)延长AM至K,使MK=AM,连接DK、EK,得平行四边形ADKE.

则EK⊥DC,∠EKD=∠EAD,∴∠KDC=∠GAD,∴∠BAG=∠ADK,易证△ABG≌△DAK,
∴BG=2AM,∠DAK=∠ABG,∴AM⊥BG.
(3)如图所示,BG=2AM,AM⊥BG.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
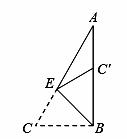
 °角的直角三角板ABC紧靠着放在同一平面内,使直角边BC与量角器的0°线CD在同一直线上(即点B、C、O、D在同一直线上),O为量角器圆弧所在圆的圆心,∠ACB=90°,∠CAB=30°, BC=6cm.
°角的直角三角板ABC紧靠着放在同一平面内,使直角边BC与量角器的0°线CD在同一直线上(即点B、C、O、D在同一直线上),O为量角器圆弧所在圆的圆心,∠ACB=90°,∠CAB=30°, BC=6cm.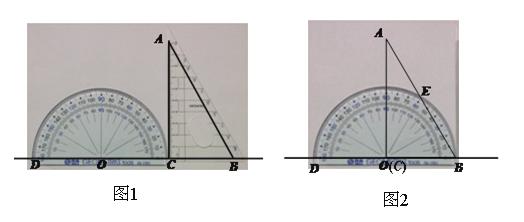
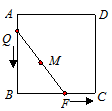


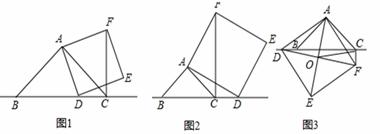
 ,对角线AE,DF相交于点O,连接OC 求OC的长度.
,对角线AE,DF相交于点O,连接OC 求OC的长度.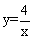 图象上,点B在反比例函数
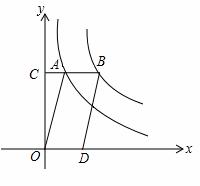
图象上,点B在反比例函数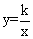 (k≠0)的图象上,CB∥x轴,BD∥AO,若CA=
(k≠0)的图象上,CB∥x轴,BD∥AO,若CA=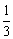 CB,则双曲线
CB,则双曲线