题目内容
已知:如图①,在边长为1的正方形ABCD中,对角线AC、BD相交于点M,直线EF经过点A,且与BD平行,点O是AC上一动点 以O为圆心,OA为半径画圆.

(1)直线EF与⊙O相切吗?请说明理由;
(2)如图②,当⊙O与BC相切于点N时 求⊙O的半径.

(1)直线EF与⊙O相切吗?请说明理由;
(2)如图②,当⊙O与BC相切于点N时 求⊙O的半径.
考点:切线的判定与性质
专题:
分析:(1)由正方形的性质可以得出∠MBA=∠MAB=45°,由BD∥EF就可以得出∠DBA=∠BAF=45°,就可以得出∠MAF=90°,进而得出结论;
(2)连结ON,就可以得出ON⊥BC,得出∠CNO=90°,由正方形的性质就可以得出∠ABC=90°,进而得出ON∥AB,就有△CON∽△CAB,就有
=
,设⊙O的半径为x,就有ON=AO=x,由勾股定理就可以得出AC=
,进而代入比例式就可以求出结论.
(2)连结ON,就可以得出ON⊥BC,得出∠CNO=90°,由正方形的性质就可以得出∠ABC=90°,进而得出ON∥AB,就有△CON∽△CAB,就有
| ON |
| AB |
| CO |
| AC |
| 2 |
解答:解:(1)EF与⊙O相切.
理由:如图1,∵四边形ABCD是正方形,
∴∠MBA=∠MAB=45°.
∵BD∥EF,
∴∠DBA=∠BAF,
∴∠BAF=45°,
∴∠CAF=90°,
∴CA⊥EF,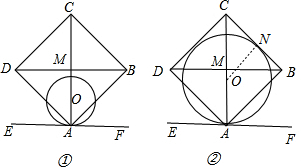
∴直线EF与⊙O相切;
(2)如图2,连结ON.
∵⊙O与BC相切于点N,
∴ON⊥BC,
∴∠CNO=90°.
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠CNO=∠ABC,
∴ON∥AB,
∴△CON∽△CAB,
∴
=
.
在Rt△ABC中,由勾股定理,得
AC=
.
设⊙O的半径为x,则有ON=AO=x,OC=
-x,
∴
=
,
解得:x=2-
.
答:⊙O的半径为2-
.
理由:如图1,∵四边形ABCD是正方形,
∴∠MBA=∠MAB=45°.
∵BD∥EF,
∴∠DBA=∠BAF,
∴∠BAF=45°,
∴∠CAF=90°,
∴CA⊥EF,

∴直线EF与⊙O相切;
(2)如图2,连结ON.
∵⊙O与BC相切于点N,
∴ON⊥BC,
∴∠CNO=90°.
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠CNO=∠ABC,
∴ON∥AB,
∴△CON∽△CAB,
∴
| ON |
| AB |
| CO |
| AC |
在Rt△ABC中,由勾股定理,得
AC=
| 2 |
设⊙O的半径为x,则有ON=AO=x,OC=
| 2 |
∴
| x |
| 1 |
| ||
|
解得:x=2-
| 2 |
答:⊙O的半径为2-
| 2 |
点评:本题考查了正方形的性质的运用,平行线的性质的运用,圆的切线的判定及性质的运用,勾股定理的运用,相似三角形的判定及性质的运用,解答时运用切线的性质求解是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
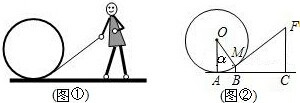 如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6.
如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6. 在四边形ABCD中,已知BC=8,CD=12,AD=10,∠A=∠B=60°,则AB=
在四边形ABCD中,已知BC=8,CD=12,AD=10,∠A=∠B=60°,则AB=