题目内容
求证：如果一个直角三角形的斜边和一条直角边的对应比相等，那么这两个三角形相似．
考点：相似三角形的判定
专题：证明题
分析：可设AB、A′B′，AC、A′C′的比为k，进而由勾股定理求出BC：B′C′的值，此时可得两三角形的三边都对应成比例，由此来得出两三角形相似的结论．
解答：证明：
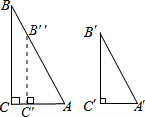
在AC上截取AC″=A′C′，过C″作C″B″∥BC交AB于B″，
在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，
=
，
设
=
，=k，则AB=kA′B′，AC=kA′C′；
在Rt△ABC和Rt△A′B′C′中，
=
=k，
∴
=
=
∴Rt△ABC∽Rt△A′B′C′．
在AC上截取AC″=A′C′，过C″作C″B″∥BC交AB于B″，
在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，
| AB |
| A′B′ |
| AC |
| A′C′ |
设
| AB |
| A′B′ |
| AC |
| A′C′ |
在Rt△ABC和Rt△A′B′C′中，
| BC |
| B′C′ |
|
∴
| AB |
| A′B′ |
| AC |
| A′C′ |
| BC |
| B′C′ |
∴Rt△ABC∽Rt△A′B′C′．
点评：此题考查的是相似三角形的判定以及全等三角形的判定和性质．能够正确的理解材料的含义，熟练掌握相似三角形的判定方法是解答此题的关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
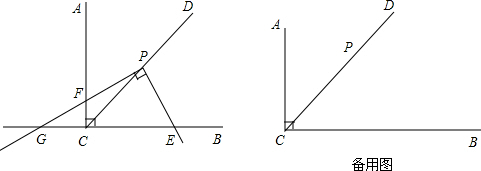
已知：AB=BC=CA，BD=DE=BE，∠1=∠2=∠3，联结AE、DC，求证：AE=DC．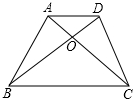
如图，梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，问：△AOB与△COD是否相似？方程2x-5=x-2的解是（ ）
| A、x=-1 | B、x=-3 |
| C、x=3 | D、x=1 |