题目内容
15.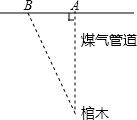 如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?
如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?
分析 先根据AB=8米,AC=24米得出tanB=$\frac{AC}{AB}$=3,求出∠B的度数,再由勾股定理求出BC的长即可.
解答 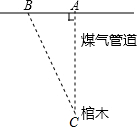 解:∵AB=8米,AC=24米,
解:∵AB=8米,AC=24米,
∴tanB=$\frac{AC}{AB}$=3,
∴∠B≈71°,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{8}^{2}+2{4}^{2}}$=8$\sqrt{10}$(米).
答:考古人员应以与地平面形成71°的角度进行挖掘才能沿最短路线挖到棺木,他们需要挖8$\sqrt{10}$米的距离.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
3.y=$\sqrt{x-3}$+$\sqrt{3-x}$+8,则3x+2y的平方根是( )
| A. | 5 | B. | -5 | C. | ±3 | D. | ±5 |
10.根据指令计算,完成如下填空:
a=-6,b=$\frac{1}{2}$,c=-2,d=-9,e=3,f=-$\frac{1}{4}$.
| 输入 | 执行操作 ×(-$\frac{1}{3}$) | 输出(入) | 执行操作 ÷(-12) | 输出(入) | 执行操作 ÷(-$\frac{1}{4}$) | 输出 |
| 18 | … | a | … | b | … | c |
| d | … | e | … | f | … | 1 |
7.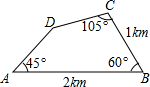 为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
 为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )| A. | $\frac{3+\sqrt{6}}{4}$km2 | B. | $\frac{3-\sqrt{6}}{4}$km2 | C. | $\frac{6+\sqrt{3}}{4}$km2 | D. | $\frac{6-\sqrt{3}}{4}$km2 |
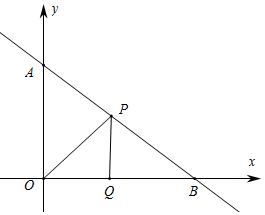
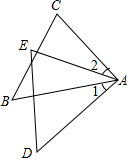 如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.
如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.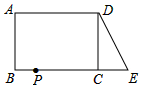 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为1或7秒时,△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为1或7秒时,△ABP和△DCE全等.