题目内容
17. 如图,△ABC中,AB=5,AD=6,AC=13,D为BC的中点,则S△ABC=30.
如图,△ABC中,AB=5,AD=6,AC=13,D为BC的中点,则S△ABC=30.
分析 延长AD到E使AD=DE,连接CE,先证明△CDE≌△BDA,则CE=5,S△ACE=S△CAB,接下来,依据勾股定理的逆定理可证明△ACE为直角三角形,最后依据S△CAB=S△ACE=$\frac{1}{2}$AE•CE求解即可.
解答 解:延长AD到E使AD=DE,连接CE.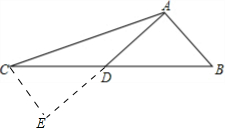
在△CDE和△BDA中$\left\{\begin{array}{l}{CD=BD}\\{∠CDE=∠ADB}\\{DE=AD}\end{array}\right.$,
∴△CDE≌△BDA.
∴CE=AB=5,S△ADB=S△CDE.
∴S△ACE=S△CAB.
在△ACE中,AC2=CE2+AE2,
∴△ACE为直角三角形.
∴S△CAB=S△ACE=$\frac{1}{2}$AE•CE=$\frac{1}{2}$×5×12=30.
故答案为:30.
点评 本题主要考查的是全等三角形的性质和判定、勾股定理的逆定理的应用,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
19.计算(-2)×3的结果是( )
| A. | -5 | B. | -6 | C. | 1 | D. | 6 |
9. 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.| A. | 16-8$\sqrt{3}$ | B. | -12+8$\sqrt{3}$ | C. | 8-4$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
 如图,矩形ABCD由3*4个小正方形组成,此图中不是正方形的矩形有40个.
如图,矩形ABCD由3*4个小正方形组成,此图中不是正方形的矩形有40个. 如图,直线l1,l2分别与另两条直线相交,已知∠1=∠2,求证:∠3+∠4=180°.
如图,直线l1,l2分别与另两条直线相交,已知∠1=∠2,求证:∠3+∠4=180°. 在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$.
在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$. 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3.
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3. 在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.