题目内容
如图，点P是矩形ABCD的边AD的一个动点，矩形的两条边AB、BC的长分别为6和8．设点P到AC的距离为x，到BD的距离为y，则x+y的值是（ ）A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
考点：矩形的性质
专题：
分析：过P点作PE⊥AC，PF⊥BD，由矩形的性质可证△PEA∽△CDA和△PFD∽△BAD，根据
=
，和
=
，两式相加得PE+PF=
，即为点P到矩形的两条对角线AC和BD的距离之和．
| PE |
| CD |
| PA |
| CA |
| PF |
| AB |
| PD |
| BD |
| 24 |
| 5 |
解答：解：过P点作PE⊥AC，PF⊥BD，
∵四边形ABCD是矩形，
∴AD⊥CD，
∴△PEA∽△CDA，
∴
=
，
∵AC=BD=
=10，
∴
=
…①，
同理：△PFD∽△BAD，
∴
=
，
∴
=
…②，
∴①+②得：
=
=
=
，
∴PE+PF=
，
即点P到矩形的两条对角线AC和BD的距离之和是
．
故选B．
∵四边形ABCD是矩形，
∴AD⊥CD，
∴△PEA∽△CDA，
∴
| PE |
| CD |
| PA |
| CA |
∵AC=BD=
| 62+82 |
∴
| PE |
| 6 |
| PA |
| 10 |
同理：△PFD∽△BAD，
∴
| PF |
| AB |
| PD |
| BD |
∴
| PF |
| 6 |
| PD |
| 10 |
∴①+②得：
| PE+PF |
| 6 |
| PA+PD |
| 10 |
| AD |
| 10 |
| 4 |
| 5 |
∴PE+PF=
| 24 |
| 5 |
即点P到矩形的两条对角线AC和BD的距离之和是
| 24 |
| 5 |
故选B．
点评：此题主要考查了矩形的性质与相似三角形的综合运用．利用三角形的相似求线段长度是初中阶段重点知识，同学们应熟练地应用好这种方法．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
如图，在平面直角坐标系xOy中，半径为5的⊙D经过原点，且与x轴、y轴交于A、B两点，点C为弧ABO上的一点（不与O、A两点重合），若点A的坐标为（6，0），则cosC的值是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
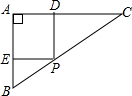如图，Rt△ABC中，∠BAC=90°，AB=3，AC=4，P是BC上一点，作PE⊥AB于E，PD⊥AC于D．设BP=x，则PD+PE等于（ ）A、4-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某几何体的三视图如图所示，则该几何体的体积为（ ）A、
| ||
| B、3π | ||
C、
| ||
| D、6π |
如图，边长为1的正方形网格中有格点△ABC（顶点是网格线的交点）和格点O，若把△ABC绕着点O逆时针旋转90°．