Question

1．已知关于x的二次函数y=ax²+bx+c（a＞0）的图象与x轴交于A，B两点，与直线y=1交于C、D两点，且点A（1，0），C（0，1）
（1）c=1；
（2）求a的取值范围；
（3）设A，B，C，D四点构成的四边形的对角线相交于点P，记△PCD的面积为S₁，△PAB的面积为S₂，求S₁-S₂的值（可以用a表示）．

Answer 1

分析 （1）把C（0，1）代入抛物线即可求出c；
（2）把A（1，0）代入得到0=a+b+1，推出b=-1-a，求出方程ax²+bx+1=0，根据判别式△=b²-4ac＞0即可求解；
（3）根据抛物线与x轴的交点的求法，求出点A、B的坐标，求出线段AB的长度，把y=1代入抛物线得到方程ax²+（-1-a）x+1=1，求出点C、D的坐标，求出线段CD的长度，过点P作MN⊥CD于M，交x轴于N，根据△CPD∽△BPA，得出两个三角形的高PN、PM的长，根据三角形的面积公式即可求出S₁-S₂的值即可．

解答 （1）解：把C（0，1）代入抛物线得：1=0+0+c，
解得：c=1．
故答案为：1．
（2）解：根据点A（1，0）在二次函数y=ax²+bx+1上，可得：0=a+b+1，
∴b=-1-a，
即ax²+（-1-a）x+1=0，
根据抛物线与x轴有两个交点，可得：b²-4ac=（-1-a）²-4a=a²-2a+1＞0，
∴a≠1，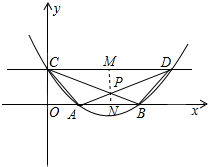
即：a的取值范围是a＞0，且a≠1；
（3）证明：∵ax²+（-1-a）x+1=0，
∴（ax-1）（x-1）=0，
∴B点坐标是（$\frac{1}{a}$，0）而A点坐标（1，0）
∴AB=$\frac{1}{a}-1=\frac{1-a}{a}$，
把y=1代入抛物线得：ax²+（-1-a）x+1=1，
解得：x₁=0，x₂=$\frac{1+a}{a}$，
∴CD=$\frac{1+a}{a}$，
如图，过P作MN⊥CD于M，交x轴于N，
则MN⊥X轴，
∵CD∥AB，
∴△CPD∽△BPA，
∴$\frac{PM}{PN}=\frac{CD}{AB}$，即：$\frac{1-PN}{PN}=\frac{\frac{1+a}{a}}{\frac{1-a}{a}}=\frac{1+a}{1-a}$，
解得：PN=$\frac{1-a}{2}$，PM=$\frac{1+a}{2}$，
∴S₁-S₂=$\frac{1}{2}•CD•PM-\frac{1}{2}•AB•PN$=$\frac{1}{2}•\frac{1+a}{a}•\frac{1+a}{2}-\frac{1}{2}•\frac{1-a}{a}•\frac{1-a}{2}$=1．

点评 本题主要考查了抛物线与x轴的交点，第（3）小题，根据相似求出三角形的高是解决此题的关键．