题目内容
11.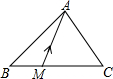 如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AM}=\overrightarrow{b}$,那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a},\overrightarrow{b}$表示)
如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AM}=\overrightarrow{b}$,那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a},\overrightarrow{b}$表示)
分析 由向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,利用三角形法则,可求得$\overrightarrow{BM}$,然后由点M在边BC上,MC=2BM,即可求得答案.
解答 解:∵向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,
∴$\overrightarrow{BM}$=$\overrightarrow{AM}$-$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∵点M在边BC上,MC=2BM,
∴$\overrightarrow{BC}$=3$\overrightarrow{BM}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$.
故答案为:3$\overrightarrow{b}$-3$\overrightarrow{a}$.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.如图所示,下列三角形中是直角三角形的是( )
| A. | 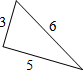 | B. | 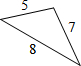 | C. | 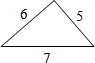 | D. |  |
19.下列分式变形中,正确的是( )
| A. | $\frac{a}{b}$=$\frac{a^2}{b^2}$ | B. | $\frac{a}{b}$=$\frac{ab}{ab}$ | C. | $\frac{a}{b}$=$\frac{a+2c}{b+2c}$(c≠0) | D. | $\frac{a}{b}$=$\frac{ac}{bc}$(c≠0) |
6.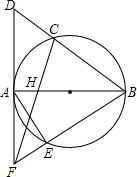 如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )
如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )
 如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )
如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )| A. | $\frac{8\sqrt{5}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
20.解方程.
(1)$\frac{10x}{2x-1}$+$\frac{5}{1-2x}$=2
(2)$\frac{1}{{x}^{2}+5x-6}$=$\frac{1}{{x}^{2}+x+6}$.
(1)$\frac{10x}{2x-1}$+$\frac{5}{1-2x}$=2
(2)$\frac{1}{{x}^{2}+5x-6}$=$\frac{1}{{x}^{2}+x+6}$.
1.$\sqrt{81}$的平方根是( )
| A. | 9 | B. | 3 | C. | ±9 | D. | ±3 |
 如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数.
如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数.