题目内容
3.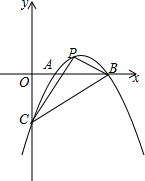 如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A、B,与y轴交于点C,点P为抛物线上一点,且∠PBO=∠CBO,求点P的坐标.
如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A、B,与y轴交于点C,点P为抛物线上一点,且∠PBO=∠CBO,求点P的坐标.
分析 利用抛物线与x轴的交点的关系解一元二次方程-$\frac{2}{5}$x2+$\frac{12}{5}$x-2=0,得抛物线与x轴的两个交点,在令x=0,求出其对应的函数值,从而求得点C的坐标,然后根据三角函数求出点P的坐标.
解答 解:令抛物线的函数值为0,则-$\frac{2}{5}$x2+$\frac{12}{5}$x-2=0,解这个二元一次方程得x1=1,x2=5
∴A(1,0),B(5,0)
又当x=0时,y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2=-2,
∴C(0,-2)
设P点的坐标为(x,-$\frac{2}{5}$x2+$\frac{12}{5}$x-2),
∵△OBC是直角三角形,∠BOC=90°,
∴tan∠OBC=$\frac{OC}{OB}$=$\frac{2}{5}$,
∵∠PBO=∠CBO,
∴tan∠PBO=$\frac{-\frac{2}{5}{x}^{2}+\frac{12}{5}x-2}{5-x}$=$\frac{2}{5}$,
化简得:x2-7x+10=0,
∴x1=2,x2=5(舍去)
∴y=$\frac{6}{5}$
∴点P的坐标为(2,$\frac{6}{5}$).
点评 本题考查了抛物线与x轴的交点问题,解题的根据是根据抛物线与x轴的交点与其解析式的关系求出抛物线与x轴的交点.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
13.已知抛物线y=x2-x-2与x轴的一个交点为(m,0),则代数式m2-m+2014的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
14.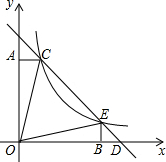 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:
①k的值为4;
②△BED是等腰直角三角形;
③S△ACO=S△BEO;
④S△CEO=15;
⑤点D的坐标为(5,0).其中正确的是( )
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;
②△BED是等腰直角三角形;
③S△ACO=S△BEO;
④S△CEO=15;
⑤点D的坐标为(5,0).其中正确的是( )
| A. | ①②③ | B. | ①②③④ | C. | ②③④⑤ | D. | ①②③⑤ |
18.如果二元一次方程ax+by+2=0有两个解$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$与$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,那么,下面四个选项中仍是这个方程的解的是( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$ |
8.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{0.5}$ | B. | $\sqrt{15}$ | C. | $\sqrt{150}$ | D. | $\sqrt{\frac{1}{15}}$ |
15.关于抛物线y=x2-2x+1,下列说法错误的是( )
| A. | 开口向上 | B. | 与x轴有一个交点 | ||
| C. | 对称轴是直线x=1 | D. | 当x>1时,y随x的增大而减小 |
12.如果|x|=5,|y|=3,且x+y>0,那么x-y的值是( )
| A. | 2或8 | B. | 2或-8 | C. | -2或8 | D. | -2或-8 |
13.计算-18÷3×(-$\frac{1}{3}$)的结果为( )
| A. | -18 | B. | 18 | C. | -2 | D. | 2 |