题目内容
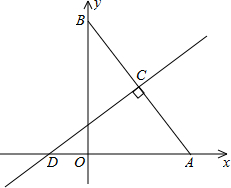 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴、y轴的正半轴上(OA<OB﹚,且AO,OB的长分别是一元二次方程x2-14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,D的坐标为(-| 3 |
| 7 |
(1)求A,B两点坐标;
(2)求直线CD的函数关系式.
考点:一次函数综合题
专题:
分析:(1)解方程求得方程的两个解,即求得A的横坐标和B的纵坐标,从而求解;
(2)在直角△PBQ中利用勾股定理求得OE的长,即E的坐标,然后利用待定系数法求得直线的解析式.
(2)在直角△PBQ中利用勾股定理求得OE的长,即E的坐标,然后利用待定系数法求得直线的解析式.
解答: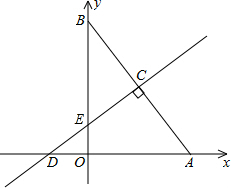 解:(1)解方程x2-14x+48=0,
解:(1)解方程x2-14x+48=0,
解得:x1=6,x2=8,
则A的坐标是(6,0),B的坐标是(0,8);
(2)令CD交y轴于点E,连接AE,设OE=x,
∵CD是线段AB的垂直平分线,
∴BE=AE=8-x,
在直角△PBQ中,OE2+AO2=AE2,则62+x2=(8-x)2,
解得:x=
,
则E的坐标是(0,
).
设直线CD的函数解析式是y=kx+b,
则-
k+b=0,b=
,
∴k=
,b=
,
则函数的解析式是:y=
x+
.
 解:(1)解方程x2-14x+48=0,
解:(1)解方程x2-14x+48=0,解得:x1=6,x2=8,
则A的坐标是(6,0),B的坐标是(0,8);
(2)令CD交y轴于点E,连接AE,设OE=x,
∵CD是线段AB的垂直平分线,
∴BE=AE=8-x,
在直角△PBQ中,OE2+AO2=AE2,则62+x2=(8-x)2,
解得:x=
| 7 |
| 4 |
则E的坐标是(0,
| 7 |
| 4 |
设直线CD的函数解析式是y=kx+b,
则-
| 7 |
| 3 |
| 7 |
| 4 |
∴k=
| 3 |
| 4 |
| 7 |
| 4 |
则函数的解析式是:y=
| 3 |
| 4 |
| 7 |
| 4 |
点评:本题是一次函数与勾股定理的综合应用,正确求得E的坐标是关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
下列各组长度的线段能构成三角形的是( )
| A、3cm,4cm,8cm |
| B、5cm,6cm,11cm |
| C、6cm,1cm,6cm |
| D、4cm,10cm,4m |
 如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,求证:AB2=AD•AC,BD2=AD•DC.
如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,求证:AB2=AD•AC,BD2=AD•DC.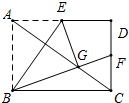 在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.
在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.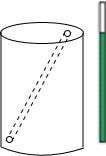 如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置)
如图所示,一个油漆桶高1m,桶内还有剩余油漆,一根木棒长1.5m,小明把木棒从桶盖小口斜插入桶内,一端触到桶底边缘时,另一端恰好与桶盖小口相齐,抽出木棒,量得木棒上浸沾油漆的部分长0.75m,那么桶内油漆面的高度是多少?(油漆桶水平放置) 如图,在△ABC中,AC=BC=2cm,∠C=90°,按下列条件建立坐标系,写出顶点的坐标.
如图,在△ABC中,AC=BC=2cm,∠C=90°,按下列条件建立坐标系,写出顶点的坐标.