题目内容
若双曲线y=
位于第二、四象限,则k的取值范围是 .
| k-1 |
| x |
考点:反比例函数的性质
专题:
分析:由反比例函数图象的位置在第二、四象限,可以得出k-1<0,然后解这个不等式就可以求出k的取值范围.
解答:解:∵双曲线y=
位于第二、四象限,
∴k-1<0,
∴k<1.
故答案为:k<1.
| k-1 |
| x |
∴k-1<0,
∴k<1.
故答案为:k<1.
点评:本题主要考查了反比例函数的图象及其性质,用到的知识点:对于反比例函数y=
来说,当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
| k |
| x |

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
下列运算正确的是( )
A、
| ||
| B、-3+8=-5 | ||
| C、-|-6|=6 | ||
| D、(-3)2=9 |
-
的倒数是( )
| 1 |
| 2 |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
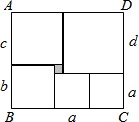 如图,长方形ABCD被分成六个小正方形,已知中间一个小正方形的边长为2,其他正方形的边长分别为a、b、c、d.观察图形并探索:
如图,长方形ABCD被分成六个小正方形,已知中间一个小正方形的边长为2,其他正方形的边长分别为a、b、c、d.观察图形并探索: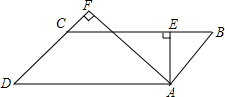 如图,已知?ABCD的周长为10
如图,已知?ABCD的周长为10