Question

14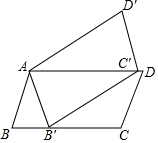．如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点），点B′恰好落在BC边上，则∠C=105°．

Answer 1

分析 利用旋转的性质得AB=AB′，∠BAB′=30°，再根据等腰三角形的性质和三角形内角和定理可计算出∠B=∠AB′B=75°，接着利用平行四边形的性质得到AD∥BC，∠BAD=∠C，则∠DAB′=∠AB′B=75°，所以∠BAD=105°，于是得到∠C=105°．

解答 解：∵平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′，点B′恰好落在BC边上，
∴AB=AB′，∠BAB′=30°，
∴∠B=∠AB′B=$\frac{1}{2}$（180°-30°）=75°，
∵四边形ABCD为平行四边形，
∴AD∥BC，∠BAD=∠C，
∴∠DAB′=∠AB′B=75°，
∴∠BAD=∠BAB′+∠DAB′=30°+75°=105°，
∴∠C=105°．
故答案为105°．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等：对应点与旋转中心所连线段的夹角等于旋转角：旋转前、后的图形全等．也考查了平行四边形的性质．