题目内容
18.(1)计算:(a-1)(a+1)=a2-1;
(a-1)(a2+a+1)=a3-1;
(a-1)(a3+a2+a+1)=a4-1;
(2)由上面的规律我们可以猜想,得到:
(a-1)(a2017+a2016+a2015+a2014+…+a2+a+1)=a2018-1;
(3)利用上面的结论,求下列各式的值.
①22017+22016+22015+22014+…+22+2+1
②52017+52016+52015+52014+…+52+5+1.
分析 (1)各式利用多项式乘以多项式法则计算得到结果即可;
(2)归纳总结得到一般性规律,确定出所求即可;
(3)各式变形后,利用得出的结论计算即可得到结果.
解答 解:(1)(a-1)(a+1)=a2-1;
(a-1)(a2+a+1)=a3-1;
(a-1)(a3+a2+a+1)=a4-1;
故答案为:a2-1;a3-1;a4-1;
(2)由上面的规律我们可以猜想,得到:
(a-1)(a2017+a2016+a2015+a2014+…+a2+a+1)=a2018-1;
故答案为:a2018-1;
(3)理利用上面的结论,求下列各式的值.
①22017+22016+22015+22014+…+22+2+1=(2-1)×(22017+22016+22015+22014+…+22+2+1)=22018-1;
②52017+52016+52015+52014+…+52+5+1=$\frac{1}{4}$(5-1)×(52017+52016+52015+52014+…+52+5+1)=$\frac{1}{4}$×(52018-1).
点评 此题考查了平方差公式,以及规律型:数字的变化类,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
 如图是在方格纸上画出的小旗图案,若用(1,1)表示点A,(1,5)表示点B,(2,3)表示点D,那么点C的位置可表示为(4,3).
如图是在方格纸上画出的小旗图案,若用(1,1)表示点A,(1,5)表示点B,(2,3)表示点D,那么点C的位置可表示为(4,3).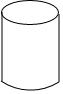 圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化.
圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化.
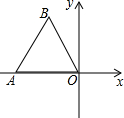 如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).